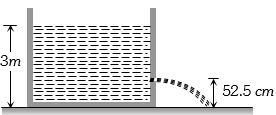
પાત્રમાં $ 3m$ ઉંચાઇ સુધી પાણી ભરેલ છે.છિદ્ર અને બીકરના આડછેદના ક્ષેત્રફળનો ગુણોત્તર $0.1 $ છે.તો છિદ્રમાંથી બહાર આવતાં પ્રવાહીના વેગનો વર્ગ ....... $m^2/s^2$ થાય. $(g = 10 m/s^2)$

IIT 2004, Diffcult
a
(a)Let \(A = \) cross-section of tank
\(a = \) cross-section hole
\(V =\) velocity with which level decreases
\(v = \) velocity of efflux
From equation of continuity \(av = AV \Rightarrow V = \frac{{av}}{A}\)
By using Bernoulli's theorem for energy per unit volume
Energy per unit volume at point A
= Energy per unit volume at point B
\(P + \rho gh + \frac{1}{2}\rho {V^2} = P + 0 + \frac{1}{2}\rho {v^2}\)
==> \({v^2} = \frac{{2gh}}{{1 - {{\left( {\frac{a}{A}} \right)}^2}}} = \frac{{2 \times 10 \times (3 - 0.525)}}{{1 - {{(0.1)}^2}}} = 50{(m/\sec )^2}\)
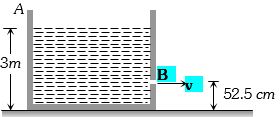
(a)Let \(A = \) cross-section of tank
\(a = \) cross-section hole
\(V =\) velocity with which level decreases
\(v = \) velocity of efflux
From equation of continuity \(av = AV \Rightarrow V = \frac{{av}}{A}\)
By using Bernoulli's theorem for energy per unit volume
Energy per unit volume at point A
= Energy per unit volume at point B
\(P + \rho gh + \frac{1}{2}\rho {V^2} = P + 0 + \frac{1}{2}\rho {v^2}\)
==> \({v^2} = \frac{{2gh}}{{1 - {{\left( {\frac{a}{A}} \right)}^2}}} = \frac{{2 \times 10 \times (3 - 0.525)}}{{1 - {{(0.1)}^2}}} = 50{(m/\sec )^2}\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પાણીથી ભરેલ ટાંકીના તળિયે કાણું છે.જો ટાંકીના તળિયે કુલ દબાણ $3\,atm$ હોય ($1\,atm$ $= 10^5\, N/m^2$),તો પ્રવાહનો વેગ કેટલો હશે?View Solution
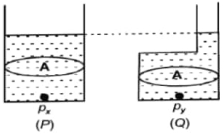
- 2આકૃતિમાં સમાન પાયાનું ક્ષેત્રફળ $A$ સાથેના બે પાત્રો $P$ અને $Q$ દર્શાવેલ છે અને દરેકને સમાન ઊંચાઈ સુધી સમાન પ્રવાહીથી ભરવામાં આવે છે. તેમને અનુરૂપ પસંદ કરો.View Solution
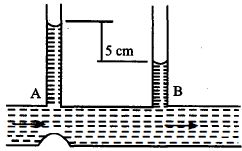
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે મેનોમીટરની બે નળી વચ્ચેનો તફાવત $5\, cm$ છે. $A$ અને $B$ નળીના આડછેડનું ક્ષેત્રફળ અનુક્રમે $6\, mm^2$ અને $10\, mm^2$ છે.તો નળીમાં પાણી ......... $ cc/s$ દરથી વહન કરતું હશે?$(g\, = 10\, ms^{-2})$View Solution
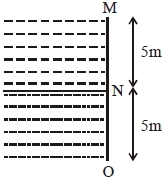
- 4આકૃતિમાં દર્શાવ્યા મુજબ $10\; \mathrm{m}$ ના ચોરસ પાત્રમાં બે પ્રવાહી ભરેલા છે જેમની ઘનતા $\rho_{1}$ અને $\rho_{2}\left(\rho_{2}=2 \rho_{1}\right)$ છે.બંને પ્રવાહીની ઊંચાઈ $5 \;\mathrm{m} .$ છે.આ પ્રવાહીના કારણે $MN$ અને $NO$ પર લાગતા બળનો ગુણોત્તર કેટલો મળે?View Solution
(પ્રવાહી એકબીજામાં મિશ્ર થતાં નથી)
- 5View Solutionવિધાન : વરસાદના ટીપાં ટર્મિનલ વેગ પ્રાપ્ત કરે છે.
કારણ : ગતિની દિશામાં લાગતું અચળ બળ અને વેગ પર આધાર રાખતું ગતિની વિરુદ્ધ દિશામાં લાગતું બળ હમેશા ટર્મિનલ વેગ પ્રાપ્ત કરે.
- 6$w$ જાડાઈ ધરાવતા અને $H$ ઊંંચાઈ ધરાવતા ડેમમાં પાણી ભરવામાં આવે છે, તો ડેમ પર લાગુ પડતું પરીણામી બળ.View Solution
- 7$M$ દળ ધરાવતા અને $d$ જેટલી ઘનતા ધરાવતા એક નાના બોલ (દડા) ને, ગ્લીસરીન ભરેલા પાત્રમાં પતન કરવામાં આવે છે ત્યારે તેની ઝડપ અમુક સમય બાદ અચળ થાય છે. જે ગ્લિસરીનની ધનતા $\frac{\mathrm{d}}{2}$ જેટલી હોય તો દડા પર લાગતું સ્નિગ્ધતા (શ્યાનતા) બળ $....$ હશે.View Solution
- 8સબમરીન દરિયામાં $d_1$ ઊંડાઈએ $5.05\times 10^6\,Pa$ દબાણ અનુભવે છે.જ્યારે તે $d_2,$ ઊંડાઈએ જાય ત્યારે તે $8.08\times 10^6\,Pa$ દબાણ અનુભવે તો $d_2 -d_1$ લગભગ ........ $m$ હશે? (પાણીની ઘનતા $= 10^3\,kg/m^3$ અને ગુરુત્વ પ્રવેગ $= 10\,ms^{-2}$ )View Solution
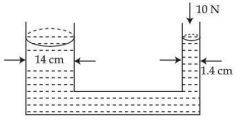
- 9આકૃતિમાં દર્શાવ્યા મુજબ ના વ્યાસ ધરાવતી બે ભુજાએમાં પાણી ભરેલું હોય તેવો હાઈડ્રોલીક પ્રેસને દર્શાવેલ છે. તેના પાતળી ભુજામાં રહેલ પાણી ઉપર $10 \mathrm{~N}$ નું બળ લગાડવામાં આવે છે. પાણીને સંતુલન સ્થિતિમાં રાખવા માટે જાડી (મોટી) ભુજામાં રહેલ પાણી ઉપર લગાવવું પડતું બળ. . . . . . $\mathrm{N}$ હશે.View Solution
- 10એક $U$ નળી જેના બંને છેડાઓ વાતાવરણ તરફ ખુલ્લા છે, તે આંશિક રીતે પાણીથી ભરેલા છે. પાણી સાથે ન ભળી જાય તેવું તેલ નળીના એક બાજુમાં ત્યાં સુધી ભરવામાં આવે છે, જયાં સુધી બીજી બાજુમાં આવેલા પાણીની સપાટીથી $10\;mm$ ઊંચાઇ પ્રાપ્ત કરી લે છે. આ દરમિયાન પાણી પોતાનો સ્તર $65 \;mm$ જેટલું વધે છે (આકૃતિ જુઓ). તેલની ઘનતા ($kg/m^3$ માં) કેટલી હશે?View Solution