પદાર્થ શરૂઆતના બિંદુ $(3,7)$ થી $4 \hat{i}$ ના અચળ પ્રવેગથી ગતિ કરે છે. $3 \;s$ બાદ તેના સ્થાન યામાક્ષો શું હશે?
Medium
c
(c)
(c)
The initial coordinate of the particle is \((3,7)\)
\(x\)-coordinate is \(3\) unit
\(y\)-coordinate is \(7\) unit
As the body starts from rest so initial velocity \(=0\)
The acceleration of the body along \(x\)-axis \(=4\) units
The acceleration of the body along \(y\)-axis \(=0\)
So, after \(3\) seconds,
Using equation of motion along \(x\)-axis,
\(x=x_0+u t+\frac{1}{2} a t^2\)
as \(u=0 \quad a=4\) units \(\quad t=3\) seconds
\(s=3+\frac{1}{2} \times 4 \times 3^2=2\) lunits
As there is no motion along \(y\)-axis so it will remain unchanged
Hence the final coordinate are \((21,7)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2 \,m$ ત્રિજ્યામાં ઇલેક્ટ્રોન $4 \,m / s$નાં વેગથી વર્તુળમય ગતિ કરે છે, તો ઇલેક્ટ્રોનનો પ્રવેગ ...... ($m / s ^{2}$ માં)View Solution
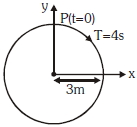
- 2વર્તુળની ત્રિજ્યા, ભ્રમણનો આવર્તકાળ, પ્રારંભિક સ્થિતિ અને ભ્રમણની દિશા આકૃતિમાં દર્શાવેલ છે. ભ્રમણ કરતાં કણ $P$ નો ત્રિજ્યા સદિશનો $y-$પ્રક્ષેપ (projection) કેટલો મળે?View Solution
- 3કોઈ સમતલ માં ગતિ કરતાં કણના યામો $x = a\cos (pt)$ અને $y(t) = b\sin (pt)$ દ્વારા આપી શકાય, જ્યાં $a,\,\,b\,( < a)$ અને $p$ એ જે તે પરિમાણ ના ધન અચળાંકો છે. તો.....View Solution
- 4$x$-અક્ષની સાપેક્ષે ગતિ કરી રહેલ કણોની સ્થિતિ $x=\left(-2 t^3\right.$ $\left.+3 t^2+5\right) \,m$ દ્વારા આપવામાં આવે છે. જે ક્ષણે કણનો વેગ શૂન્ય બને છે ત્યારે કણનો પ્રવેગ ........... $m / s ^2$ થાય?View Solution
- 5એક પદાર્થ $P$ વર્તુળાકાર પથ પર $a$ ત્રિજયામાં $v$ ઝડપથી વર્તુળમય ગતિ કરે છે.$c$ એ વર્તુળનું કેન્દ્ર છે,અને $AB$ વ્યાસ છે.જયારે કણ $B$ પાસેથી પસાર થાય,ત્યારે $A$ અને $C$ ની સાપેક્ષે તેના કોણીય વેગનો ગુણોત્તર કેટલો થાય?View Solution
- 6રામ $6 \,m / s$ ની ઝડપે પૂર્વ દિશામાં ગતિ કરે છે અને શ્યામ ઉત્તર-પૂર્વના $30^{\circ}$ ના ખૂણે $6 \,m / s$ ની ઝડપે ગતિ કરે છે. તો તેના સાપેક્ષ વેગનું મુલ્ય ............. $m / s$ થાય ?View Solution
- 7$70\,m$ ઊંચાઇ ધરાવતા ટાવર પરથી $50\,m/s$ ના વેગથી $30^o$ ના પ્રક્ષિપ્તકોણે ફેંકેલો પદાર્થ ........ $(\sec)$ સમયમાં જમીન પર આવશે.View Solution
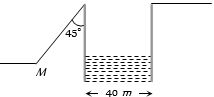
- 8પદાર્થને ઘર્ષણરહિત ઢાળ(લંબાઇ = $20\sqrt 2 \,m$) પર $M$ બિંદુથી $u$ વેગથી પ્રક્ષિપ્ત કરતા તે $45^o$ ના ખૂણે $40 \,m $ના કુવાને પાર કરે તો $M$ બિંદુ પાસે તેનો વેગ કેટલો હોવો જોઈએ?View Solution
- 9View Solutionએક ટ્રેન ઉત્તર દિશામાં ગતિ કરે છે. એક જગ્યાએથી તે ઉત્તર-પૂર્વ દિશામાં વળાંક લે છે, તો એવું તારણ કાઢી શકાય કે....
- 10એક ટેબલ પરથી એક પદાર્થને $4 \,m/sec$ ના સમક્ષિતિજ વેગથી ફેંકતા તે જમીન પર $0.4\, sec$ એ આવે છે,તો નીચેનામાંથી શું સાચું છે .View Solution
