પદાર્થ સરળ આવર્ત ગતિ કરે છે. સ્થિતિઉર્જા $(P.E.)$, ગતિઉર્જા $(K.E.)$ અને કુલઉર્જા $(T.E.)$ સ્થાનતર $x$ ના વિધેય સ્વરૂપે માપવામાં આવે છે. નીચેનામાંથી કયું વિધાન સાચું છે?
AIEEE 2003, Easy
Download our app for free and get started
b
(b) In \(S.H.M.,\) at mean position i.e. at \(x = 0\) kinetic energy will be maximum and \(PE\) will be minimum. Total energy is always constant.
(b) In \(S.H.M.,\) at mean position i.e. at \(x = 0\) kinetic energy will be maximum and \(PE\) will be minimum. Total energy is always constant.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સરળ આવર્ત ગતિ કરતાં કણ માટે મહત્તમ પ્રવેગ અને વેગનો ગુણોત્તર $10\,s^{-1}$ છે. $t = 0$ સમયે તેનું સ્થાનાંતર $5\, m$ હોય તો તેનો મહત્તમ પ્રવેગ કેટલો હશે? શરૂઆતની કળા $\frac{\pi }{4}$ છે.View Solution
- 2એક ઘડિયાળ $S$ એક સ્પ્રિંગના દોલનોને આધારે છે. જ્યારે બીજી ઘડિયાળ $P$ સાદા લોલકને આધારે છે. બંને ઘડિયાળ પૃથ્વીના દર મુજબ જ ફરે છે. તે બંનેને પૃથ્વી જેટલી જ ઘનતા પરંતુ પૃથ્વીથી બે ગણી ત્રિજ્યા ધરાવતા ગ્રહ પર લઈ જવામાં આવે તો ક્યું વિધાન સત્ય છે ?View Solution
- 3સરળ આવર્ત ગતિ કરતાં પદાર્થની કુલઊર્જા $E$ છે,તો સમતોલન સ્થાનથી કંપવિસ્તારના અડધા અંતરે ગતિઊર્જા કેટલી થાય?View Solution
- 4જ્યારે $m$ જેટલા દળને સ્પ્રિંગ સાથે જોડવામાં આવે છે. ત્યારે તે $4 \,s$ ના આવર્તકાળથી દોલન કરે છે. જ્યારે વધારાનું $2 \,kg$ દળ જોડવામાં આવે છે. તો તેનો આવર્તકાળ $1\, s$ જેટલો વધે છે. તો $m$ નું મુલ્ય ......... $kg$View Solution
- 5સાઇનસૉઇડલ તરંગમાં કોઈ નિશ્ચિત બિંદુને મહત્તમ સ્થાનાંતરથી શૂન્ય સ્થાનાંતર સુધી જવા માટે $0.17 \,sec$ નો સમય લાગે છે. આ તરંગની આવૃત્તિ ($Hz$ માં) કેટલી હશે?View Solution
- 6જ્યારે સરળ આવર્ત ગતિ કરતાં પદાર્થની સ્થિતિઊર્જા દોલન દરમિયાન તેના મહત્તમ મૂલ્યના ચોથા ભાગની થાય, ત્યારે સમતોલન સ્થાનથી સ્થાનાંતર તેના કંપવિસ્તાર $a$ ના પદમાં કેટલું હશે?View Solution
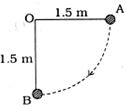
- 7એક લોલકના ગોળાનું દળ $50 gm $ છે. આ ગોળાને આકૃતિમાં દર્શાવ્યાં પ્રમાણે સમક્ષિતિજ સપાટી $A$ પરથી મુક્ત કરવામાં આવે છે. જો આ લોલકની લંબાઈ $1.5 m$ હોય, તો તે જયારે ગતિપથના સૌથી નીચેના બિંદુ $B $ પાસે પહોંચે ત્યારે તેની ગતિ-ઊર્જા કેટલી હશે ? ($g = 10 m/s^2$ લો.)View Solution
- 8સરળઆવર્ત ગતિ કરતા કણનું સ્થાંનાતર $ y = 4{\cos ^2}(t/2)\sin (1000t) $ મૂજબ છે.તો તેમાં કેટલી સરળઆવર્ત ગતિ મિશ્ર છે?View Solution
- 9$m x^{2}-b x+k=0$View Solution
અવમંદિત દોલનોમાં ઊર્જા મહતમ ઊર્જાથી અડધી કેટલા સમયે થાય.
- 10સાદુ લોલક $2 \,sec$ ના આવર્તકાળથી દોલનો કરે છે,સમતોલન સ્થાન પાસે દોરીમાં તણાવ કેટલો થાય?View Solution
