પ્લેટફોર્મ પર રહેલ ધ્વનિ ઉદ્ગમની આવૃત્તિ $5 kHz$ છે.સાઇરન તરફ આવતી ટ્રેન $A$ માં બેઠેલ પેસેન્જરને સંભળાતી આવૃત્તિ $5.5 kHz$ છે. જયારે આ વ્યકિત પોતાની યાત્રા પૂરી કરીને ટ્રેન $B$ માં પાછો આવે,ત્યારે સંભળાતી આવૃત્તિ $6 kHz$ છે,તો $ B$ અને $A$ ટ્રેન ના વેગનો ગુણોત્તર કેટલો થાય?
IIT 2002, Difficult
Download our app for free and get started
b
(b) In both the cases observer is moving towards, the source.
(b) In both the cases observer is moving towards, the source.
Hence by using \(n' = n\left( {\frac{{v + {v_0}}}{v}} \right)\)
When passenger is sitting in train \(A\), then
\(5.5 = 5\left( {\frac{{v + {v_A}}}{v}} \right)\) …\((i)\)
when passenger is sitting in train \(B\), then
\(6 = 5\left( {\frac{{v + {v_B}}}{v}} \right)\) …\((ii)\)
On solving equation \((i)\) and \((ii)\) we get \(\frac{{{v_B}}}{{{v_A}}} = 2\)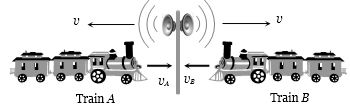
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક ધ્વનિશોષક કોઈ ધ્વનિનું પ્રમાણ $20\; dB$ ઘટાડે છે. તો આ ધ્વનિની તીવ્રતામાં કેટલા ગણો ધટાડો થાય?View Solution
- 2સમાન તણાવ ધરાવતા સોનોમીટરના તારની મૂળભૂત આવૃત્તિ $500 Hz$ છે,એક તારમાં તણાવ કેટલું .... $\%$ વધારતાં $5$ સ્પંદ સંભળાય $?$View Solution
- 3દીવાલ તરફ $72 \,km/hr$ ના વેગથી જતી કાર $124\,vib/sec$ ની આવૃત્તિવાળો હોર્ન વગાડતાં ડ્રાઇવરને કેટલી .... $vibration/sec$ આવૃત્તિ સંભળાશે? (હવામાં ધ્વનિની ઝડપ = $330 \,ms^{-1})$View Solution
- 4$512 \;Hz $ ની આવૃતિ ધરાવતો સ્વરકાંટો પિયાનોના તાર સાથે $4$ સ્પંદ પ્રતિ સેકન્ડ ઉત્પન્ન કરે છે. જ્યારે પિયાનોના તારમાં તણાવમાં થોડોક વધારવામાં આવે ત્યારે તે ઘટીને $2$ સ્પંદ પ્રતિ સેકન્ડ થાય છે. ઉત્પન્ન થાય છે. તારમાં તણાવ વધાર્યા પહેલાની આવૃત્તિ ($Hz$ માં)કેટલી હશે?View Solution
- 5$99\, cm$ અને $100\, cm$ તરંગલંબાઈ ધરાવતા બે તરંગોની ઝડપ $396\, m/s$ છે, તેમના દ્વારા એક સેકન્ડમાં ઉત્પન્ન થતાં સ્પંદ કેટલા હશે?View Solution
- 6$ {10^o} C$ તાપમાને બે બિંદુ વચ્ચેથી તરંગ પસાર થતા $2\, sec$ લાગે છે,તો $ {30^o}C $ તાપમાને તે બે બિંદુ વચ્ચેથી તરંગ પસાર થતા કેટલો ..... $sec$ સમય લાગે?View Solution
- 7બંને છેડે ખુલ્લી હોય તેવી એક નળાકાર નળીની હવામાં મૂળભૂત આવૃત્તિ $f_0$ છે. આ નળીને પાણીમાં ઊભી ડૂબાડતા અડધી નળી સુધી પાણી ભરાય છે. હવે હવાનાં સ્તંભની મૂળભૂત આવૃત્તિ કેટલી થાય?View Solution
- 8$100cm$ અને $101cm$ લંબાઇની બે બંધ પાઇપની મૂળભૂત આવૃત્તિ દ્વારા $20 sec$ માં $16$ સ્પંદ સંભળાય છે.તો ધ્વનિનો વેગ કેટલો .... $ms^{-1}$ થાય?View Solution
- 9એક ઝડપી મોટરસાયકલ ચાલક તેની આગળ ટ્રાફિક જામ જુએ છે. તે $36 \;km/hr $ સુધી ધીમો પડે છે. તેને લાગે છે કે ટ્રાફિક હળવી પડે છે અને તેની આગળ $18\; km/hr $ ની ઝડપથી જતી એક કાર $1392\; Hz$ ની આવૃત્તિનો હોર્ન વગાડી રહી છે. જો હવામાં ધ્વનિની ઝડપ $343 \;m s^{-1}$ હોય, તો તેના દ્વારા સાંભળતી હોર્નની આવૃત્તિ કેટલી હશે?View Solution
- 10બે એંજિન વિરુદ્ધ દિશામાં અચળ $30\,m/s$ ના વેગથી ગતિ કરે છે. તેમાથી એક હોર્ન વગાડે છે જેની આવૃતિ $540\,Hz$ છે. બંને એકબીજાને ક્રોસ કરે તે પહેલા બીજા એંજિનના ડ્રાઇવર દ્વારા કેટલા $Hz$ની આવૃતિવાળો અવાજ સંભળાશે? ધ્વનિની ઝડપ $330\,m/sec$ છે.View Solution