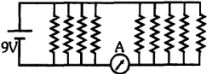
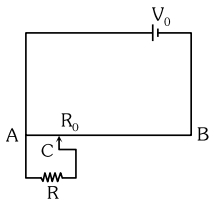
પરિપથમાં દર્શાવ્યા મુજબ સરકતો સંપર્ક $C$ પોટેન્શિયોમીટર તાર $( AB )$ ના $A$ થી લંબાઇના ચોથા ભાગ પર છે. જો તાર $AB$ નો અવરોધ $R _0$ હોય, તો પછી અવરોધ $R$ વચ્ચેનો સ્થિતિમાનનો ઘટાડો $( V )$ કેટલો હશે?

NEET 2022, Medium
a
In series, potential divides in direct ratio of resistance,
In series, potential divides in direct ratio of resistance,
So, \(V_{A C}=\frac{R_{A C}}{R_{A C}+R_{C B}} V_0\)
\(=\frac{\frac{ RR _0}{4 R + R _0}}{\frac{ RR _0}{4 R + R _0}+\frac{3 R _0}{4}} \times V _0=\frac{4 RV _0}{16 R +3 R _0}\)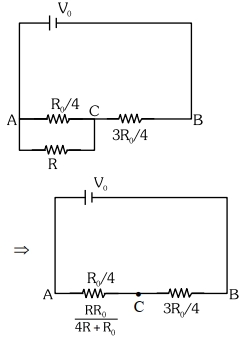
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સમાન દ્રવ્ય ધરાવતા તારની ત્રિજયાનો ગુણોત્તર $1 : 2$ અને પ્રવાહનો ગુણોત્તર $4 : 1$ હોય,તો ડ્રિફટ વેગનો ગુણોત્તર કેટલો થાય?View Solution
- 2$2 \,volt \, emf$ અને $ 5\,\Omega$ અવરોધ ધરાવતા કોષને $100 \,cm$ લંબાઇ અને $ 15 \,\Omega$ અવરોધ ધરાવતા તાર સાથે જોડવામાં આવતાં વિદ્યુતસ્થિતિમાન પ્રચલન કેટલું થાય?View Solution
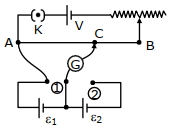
- 3આપેલ પોટેન્ટિયોમીટર પરિપથની ગોઠવણીમાં, તટસ્થ બિંદુ માટે ${AC}$ ની લંબાઈ $250\;cm$ માપવામાં આવે છે. જ્યારે ગેલ્વેનોમીટરનું જોડાણ આકૃતિમાં રહેલ બિંદુ $(1)$ થી બિંદુ $(2)$ પર કરવામાં આવે ત્યારે સંતુલન લંબાઈ $400\, {cm}$ થાય છે. બે કોષોના $e.m.f.$ નો ગુણોત્તર, $\frac{\varepsilon_{1}}{\varepsilon_{2}}$ કેટલો હશે?View Solution
- 4એક વિધુત કિટલીમાં બે ફિલામેન્ટ છે. તે પૈકીનો પ્રથમ ફિલામેન્ટ અમુક પાણીને $10$ મિનિટમાં ઉકળતું કરે છે અને બીજો ફિલામેન્ટ તેને $15$ મિનિટમાં ઉકળતું કરે છે. બંને ફિલામેન્ટને સમાંતર જોડાતાં હવે આ પાણી .............. મિનિટમાં ઉકળવા લાગશે.View Solution
- 5નીચેના પરીપથમાં દરેક અવરોધનું મૂલ્ય $10\, \Omega$ ની હોય તો $AD$ માંથી વહેતો પ્રવાહ.... હશે.View Solution
- 6View Solutionતારનો વ્યાસ ખેંચીને અડધો કરતાં અવરોધ કેટલા ગણો થાય?
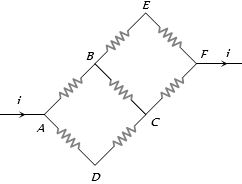
- 7આપેલ પરિપથમાં $A$ અને $B$ બિંદુ વચ્ચેનો સમતુલ્ય અવરોધ કેટલા ............. $\Omega$ થાય?View Solution
- 8એક વિધુતકોષ વડે અવરોધ $R_1$ માંથી $t$ સમય માટે વિધુતપ્રવાહ પસાર કરવામાં આવે છે. હવે આ જ કોષ વડે આટલા જ સમય માટે અવરોધ $R_2$ માંથી વિધુતપ્રવાહ પસાર કરવામાં આવે છે. આ બંને કિસ્સામાં ઉત્પન્ન થતી જૂલ ઉષ્મા સમાન હોય તો વિધુતકોષનો આંતરિક અવરોધ ...... છે.View Solution
- 9એક કાર્બન અવરોધકનો વર્ણા સંકેત $(colour\,code)$ પરથી અવરોધ $(22000 \pm 5 \%)\,\Omega$ શોધવામાં આવે છે. ત્રીજા પટ્ટાનો રંગ $......$ હોવો જોઈએ.View Solution
- 10જો આકૃતિમાંના પ્રત્યેક અવરોધ $9\, \Omega$ ના હોય તો એમિટરનું અવલોકન (વાંચન) .............. $A$ છે.View Solution