એક વિધુત કિટલીમાં બે ફિલામેન્ટ છે. તે પૈકીનો પ્રથમ ફિલામેન્ટ અમુક પાણીને $10$ મિનિટમાં ઉકળતું કરે છે અને બીજો ફિલામેન્ટ તેને $15$ મિનિટમાં ઉકળતું કરે છે. બંને ફિલામેન્ટને સમાંતર જોડાતાં હવે આ પાણી .............. મિનિટમાં ઉકળવા લાગશે.
Medium
b
વાલ્ટેજ \(V\) આપતાં બન્ને ફિલામેન્ટ પાવર \(P_1\) અને \(P_2\) લે છે.
વાલ્ટેજ \(V\) આપતાં બન્ને ફિલામેન્ટ પાવર \(P_1\) અને \(P_2\) લે છે.
અહીં, ઉષ્મા \({\text{H = }}{{\text{P}}_{\text{1}}}{{\text{t}}_{\text{1}}}{\text{ = }}{{\text{P}}_{\text{2}}}{{\text{t}}_{\text{2}}}{\text{ = (}}{{\text{P}}_{\text{1}}}{\text{ + }}{{\text{P}}_{\text{2}}}{\text{)t}}\,\) તથા \({P_1}\, = \,\,\frac{H}{{{t_1}}}\,\,\) તથા \({P_2}\, = \,\,\frac{H}{{{t_2}}}\)
\(\therefore \,\,t\,\, = \,\,\frac{H}{{{P_1} + {P_2}}}\,\,\)
\( = \,\,\frac{H}{{\frac{H}{{{t_1}}} + \frac{H}{{{t_2}}}}}\)
\( = \,\,\frac{1}{{\frac{1}{{{t_l}}} + \frac{1}{{{t_2}}}}}\,\, = \,\,\frac{{{t_1} \times {t_2}}}{{{t_1} + {t_1}}}\)
\( = \,\,\frac{{10 \times 15}}{{10 + 15}}\,\, = \,\,6\,\,\) મિનિટ
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બેટરીના બે ધ્રુવો સાથે વોલ્ટમીટર લગાડતા તેનું અવલોકન $5\,V$ છે. જ્યારે એમીટર લગાડતા તેનું અવલોકન $10\, A$ છે. $2$ ઓહમના અવરોધને આ કોષના બે છેડા સાથે જોડવામાં આવે તો તેમાંથી પસાર થતો પ્રવાહ ...........$A$ હશે.View Solution
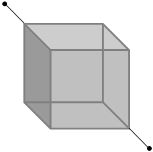
- 2સમાન લંબાઈ તથા સમાન આડછેદનું ક્ષેત્રફળ ધરાવતા $R$ વાયરો એક સમધન બનાવે છે, જો દરેક વાયરનો અવરોધ $R$ હોય તો વિકર્ણના બે છેડા વચ્ચેનો અસરકારક અવરોધ.... હશે.View Solution
- 3$\varepsilon\; emf$ અને $ r$ આંતરિક અવરોધનો એક કોષ ચલિત બાહ્ય અવરોધ $R$ સાથે જોડેલ છે. કયો આલેખ એ $R$ ની સાપેક્ષે કોષનો ટર્મિનલ વોલ્ટેજ $V $ આપે છે.View Solution
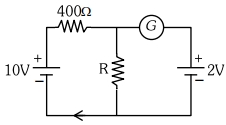
- 4જો પરિપથમાં ગેલ્વેનોમીટર $G$ કોઈ આવર્તન દર્શાવતુ ન હોય તો $R$નું મૂલ્ય $..........\,\Omega$ થાય.View Solution
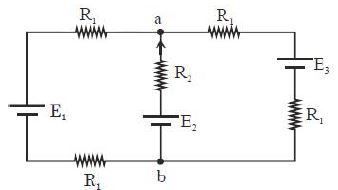
- 5આપેલ પરિપથમાં ${R_1} = 1.0\,\Omega $, ${R_2} = 2.0\,\Omega $, ${E_1} = 2\,V$ અને ${E_2} = {E_3} = 4\,V$ હોય તો બિંદુ $‘a’$ અને $‘b’$ વચ્ચે વિદ્યુતસ્થિતિમાનનો તફાવત કેટલો મળે?View Solution
- 6View Solutionનીચેનામાંથી કયો વિકલ્પ પાવરનો એકમ નથી ?
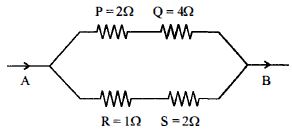
- 7જ્યારે પ્રવાહ $A$ થી $B$ તરફ વહેતો હોય ત્યારે નીચે પૈકી ચાર અવરોધ $P, Q, R$ અને $S$ માથી કયો અવરોધ મહત્તમ ઉષ્મા ઉત્પન્ન કરે?View Solution
- 8પ્રાથમિક કોષનું $e.m.f$ $2\,V$ છે જ્યારે તેને શોર્ટ કરવામાં આવે છે ત્યારે તે $4\ A$ નો વિધુતપ્રવાહ આપે છે. તો પ્રાથમિક કોષનો આંતરિક અવરોધ ............. $\Omega$ ગણો.View Solution
- 9એક તારમાંથી વહેતો વિધુતપ્રવાહ સમય સાથે $I = 3t^2 + 2t + 5$ સૂત્ર પ્રમાણે બદલાય છે, તો તારના કોઇ આડછેદમાંથી $t = 0$ થી $t = 2$ સેકન્ડના ગાળામાં પસાર થતો વિધુતભાર ........... $C$ થાય.View Solution
- 10કોષને $ 2\,Ω$ અવરોધ સાથે જોડતાં $0.5\, A $ અને $ 5\,Ω $ સાથે જોડતાં $0.25 \,A$ પ્રવાહ પસાર થાય છે,તો કોષનો $ emf$ કેટલા .............. $volt$ થાય?View Solution
