પ્રકાશની હાજરીમાં સંયોજન $(E)$ માંથી બ્રોમીનેશન પ્રક્રિયા દરમ્યાન કયો હાઇડ્રોજન સહેલાયથી વિસ્થાપિત થશે?
$\mathop {C{H_3} - }\limits_\delta \mathop {C{H_2} - }\limits_\gamma \mathop {CH = }\limits_\beta \mathop {C{H_2}}\limits_\alpha $
$(E)$
JEE MAIN 2019, Diffcult
Download our app for free and get started
b
Allylic radical will form in presence of sunlight
Allylic radical will form in presence of sunlight
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionપ્રક્રિયામાં ઉદભવતી નીપજ કઈ છે ?
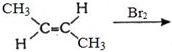
- 2મુખ્ય નિપજો $A$ અને $B$ ક્રમશ: શોધો.View Solution
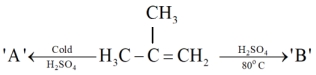
- 3View Solutionમેસો-ડાયબ્રોમોબ્યુટેનના ડિબ્રોમિનેશન દરમિયાન,કયુ મુખ્ય સંયોજન રચાય છે?
- 4View Solutionટોલ્યુઇનનું નાઇટ્રેશન....... સ્થાનમાં થાય છે.
- 5View Solutionઝાયલીનનો કયો સમઘટક ત્રણ જુદા જુદા મોનોક્લોરો વ્યુત્તપણ આપી શકે છે
- 6View Solutionનીચેનામાંથી કયા સંયોજનમાંથી હાઇડ્રોજીનેશન પર પ્રકાશઅક્રિયાશીલ સંયોજન ઉત્પન્ન થાય છે
- 7$2-$ હેક્ઝીનને ટ્રાન્સ$-2-$હેક્ઝેનમાં રૂપાંતરણ કરવા માટે નીચેનામાંથી કયું ઉપયોગ થાય છે?View Solution
- 8બેન્ઝિનનુ $500\,^oC$ તાપમાને $V_2O_5$ ની હાજરીમાં ઉદીપકીય ઓક્સિડેશન કરતા .......... મળે છે.View Solution
- 9View Solutionએરોમેટિક કેન્દ્રના ક્લોરિનેશનમાં ક્યો ઘટક ઉત્પન્ન થાય છે ?
- 10View Solutionમુક્ત મુલક વિસ્થાપન પ્રક્રિયામાં કયો આલ્કેન ઓછો પ્રક્રિયાશીલ છે ?