પ્રક્રિયા $A(g) \to A(l)$ માટે $\Delta H = - 3RT$ છે. તો પ્રક્રિયા માટે સાચો સંબંધ જણાવો.
JEE MAIN 2017, Diffcult
Download our app for free and get started
d
\(A(g) \to A(1)\)
\(A(g) \to A(1)\)
\(\Delta H = \Delta U + \Delta {n_g}RT\)
Given, \(\Delta H = - 3RT\)
Here
\(\Delta {n_g} = {n_p} - {n_r} = 0 - 1 = - 1\)
\(\Delta H = \Delta U - RT\)
\( \Rightarrow - 3RT = \Delta U - RT\)
\( \Rightarrow - 3RT + RT = \Delta U\)
\( \Rightarrow - 2RT = \Delta U\)
\(|\Delta H|\, > \,|\Delta U|\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$300 K$ અને $1 \,bar$ દબાણ પર એક મોલ મેગ્નેશિયમને ખૂલ્લા પાત્રમાં દહન માટે, $\Delta_{ C } H ^{\ominus}=-601.70 \,kJ\, mol^{-1}$, પ્રક્રિયા માટે આંતરિક ઉર્જા ફેરફારની માત્રા $kJ$ છે. (નજીકનો પૂર્ણાંક)View Solution
(આપેલ : $R =8.3\, J \,K ^{-1} \,\,mol ^{-1}$ )
- 2View Solutionઉષ્માશોષક પ્રક્રિયા કઈ છે?
- 3View Solutionઉષ્માગતિશાસ્ત્ર મુજબ પ્રક્રિયા પ્રતિવર્તીં કયારે કહી શકાય ?
- 4આપેલ આક્રૂતિને ધ્યાનમાં લો.View Solution
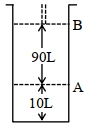
$18^{\circ} \mathrm{C}$ પર, સ્થાન $A$ પર, પિસ્ટન સાથે જોડેલા (fitted) સિલિન્ડર માં આદર્શ વાયુનો $1$ $\mathrm{mol}$ રાખેલ છે. જો તાપમાન માં કોઈપણ જાતનો ફેરફાર ન કરીએ તો પિસ્ટન એ સ્થાન $B$ તરફ ખસે છે ત્યારે આ પ્રતિવર્તી પ્રક્રમ માં થયેલ કાર્ય $'x' L atm$ છે. $x=-$ ........... $L.atm$ (નજીક નો પૂર્ણાક)
[આપેલ : નિરપેક્ષ તાપમાન $={ }^{\circ} \mathrm{C}+273.15, \mathrm{R}=0.08206 \mathrm{~L} \mathrm{~atm} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$ ]
- 5જ્યારે $6.80 \,g$ $NH_3$ ને ગરમ $CuO $ પરથી પસાર કરવામાં આવે તો એન્થાલ્પીનો ફેરફાર કેટલો થાય $?$ અહિ $NH_3$ $_{(g)}$, $CuO$$_{(s)}$ અને $H_2O$$_{(l)}$ ની પ્રમાણિત એન્થાલ્પી ઉષ્મા અનુક્રમે $-46.0$, $55.0$ અને $-285.0\, kJ\, mol$ $^{-1}$ છે. અને પ્રક્રિયા,View Solution
$N{H_{3(g)}}\, + \,\,\frac{3}{2}\,Cu{O_{(s)}}\, \to \,\,\frac{1}{2}\,{N_{2(g)}}\, + \,\,\frac{3}{2}{H_2}{O_{(\ell )}}\, + \,\,\frac{3}{2}\,C{u_{(s)}}.$ ......$J$
- 6પ્રાણાલીની આંતરિક ઉર્જા $U_1$ છે, તો બહારથી $450\, J$ ઉષ્મા લે છે અને $600\, J$ કાર્ય પુરૂ કરે છે તો પ્રાણાલીની અંતિમ ઉર્જા .......View Solution
- 7$Na _{( g )}$ માંથી $Na ^{+}$ ઉત્પન્ન થવાની આયનીકરણ એન્થાલ્પી $495.8\, kJ\, mol-1$ છે, જ્યારે $Br$ ની ઈલેક્ટ્રોન પ્રાપ્તિ એન્થાલ્પી $-325.0\, kJ\,mol^{-1}$ છે. $NaBr$ ની લેટાઈસ એન્થાલ્પી $-728.4\, kJ\, mol^{-1}$ આપેલ છે. તો આયોનીક ઘન $NaBr$ ની સર્જનમાટેની ઊર્જા $(-)$ ......... $\times 10^{-1} ,kJ \,mol ^{-1}$ છેView Solution
- 8નીચેના પૈકી ક્યા સમીકરણ માટે $\Delta H_{{\rm{react}}}^o$ નું મૂલ્ય નીપજ માટેના $\Delta H_f^o$ જેટલું હશે ?View Solution
- 9$298\,K$ એ $N_{2(g)} + 3H_{2(g)} \rightarrow 2NH_{3(g)}$ પ્રક્રિયા માટે એન્થાલ્પી ફેરફાર ($\Delta H$) $-92.38\, kJ$ છે. તો $298\,K$ એ આંતરિક ઉર્જાનો ફેરફાર ($\Delta U$) કેટલા ...... $kJ$ હશે ?View Solution
- 10પ્રક્રિયા $X_{2(g)} + 4Y_{2(g)} \rightleftharpoons XY_{4(g)}$ માટે $\Delta H$નું મૂલ્ય શૂન્યથી ઓછું છે. $XY_{4(g)}$ ની રચના તરફેણ કરવામાં આવશે,...View Solution