પ્રક્ષેપિત પદાર્થને કેટલા અંશના ખૂણે $20 \,ms ^{-1}$ ના વેગે ઉપર ફેકવો જોઈએ કે જેથી તે $10\, m$ ની ઊચાઈ સુધી પહોચી શકે?
Easy
Download our app for free and get started
c
(c)
(c)
\(H =\frac{ u ^2 \sin ^2 \theta}{2 g }\)
\(10=\frac{20 \times 20 \sin ^2 \theta}{20}\)
\(\sin ^2 \theta=\frac{1}{2}\)
\(\sin \theta=\sqrt{\frac{1}{2}}\)
\(\theta=45^{\circ}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પ્રક્ષિપ્તની કોઈ એક જગ્યા (સ્થાને) મહત્તમ ઉંયાઈ $64 \mathrm{~m}$ છે. જો પ્રારંભિંક વેગ અડધો કરવામાં આવે તો પ્રક્ષિપ્ત પદાર્થની નવી મહત્તમ ઉંચાઈ. . . . . . .$\mathrm{m}$થશે.View Solution
- 2બે ગોળીને એક સાથે $100 \;\mathrm{m}$ દૂર રહેલી $200 \;\mathrm{m}$ ઊંચાઈના બિલ્ડીંગ પરથી એકબીજા સામે સમક્ષિતિજ રીતે સમાન વેગ $25\; \mathrm{m} / \mathrm{s}$ થી છોડવામાં આવે છે. તો તે બંને ક્યારે અને ક્યાં અથડાશે? $\left(g=10 \;\mathrm{m} / \mathrm{s}^{2}\right)$View Solution
- 3એક બિંદુ પરના સ્થાન સદીશ $2 \hat{i}+4 \hat{j}$ થી બીજુ બિંદુ પરના સ્થાન સદીશ $5 \hat{i}+1 \hat{j}$ સુધીનું કણનું સ્થાનાંતર ............ એકમ હશે.View Solution
- 4એક વસ્તુ અચળ ઝડપે $10\,m$ ત્રિજ્યાના વર્તુળમાં ગતિ કરે છે.વસ્તુ $4\,sec$ માં એક પરિભ્રમણ કરે છે.ત્રીજી સેકન્ડને અંતે વસ્તુનું તેના પ્રારંભિક સ્થાનથી સ્થાનાંતર (મીટર/માં) $.........$ છે.View Solution
- 5View Solutionએક કણ વર્તુળાકાર પથ પર ઘટતી ઝડપે ગતિ કરે છે. તો નીચેનામાથી શું સાચું છે?
- 6View Solutionજો નિયમિત વર્તુળાકાર ગતિ કરતા પદાર્થની આવૃત્તિ બમણી થાય તો તેનો પ્રવેગ કેટલો થાય ?
- 7જો $R$ અને $H$ એ પ્રક્ષેપિત પદાર્થ માટે સમક્ષિતિજ વિસ્તાર અને મહત્તમ ઊંચાઈ રજૂ કરતાં હોય, તો નીચેનામાથી કયું સમીકરણ અસ્તિત્વ ધરાવે?View Solution
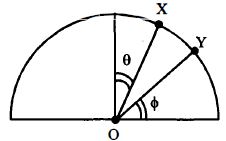
- 8એક કણને ઊભા લીસ્સા અર્ધવર્તુળાકાર માર્ગ પર બિંદુ $X$ થી એવી રીતે મુક્ત કરવામાં આવે છે કે જેથી $OX$ એ શિરોલંબ સાથે નો ખૂણો બનાવે (આકૃતિ જુઓ). માર્ગ પર ની સામાન્ય પ્રક્રિયા ને લીધે કણ બિંદુ $Y$ પાસે નાબૂદ થાય છે જ્યાં $OY$ એ સમક્ષિતિજ સાથે $\phi $ નો ખૂણો બનાવે છે. તો .....View Solution
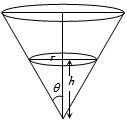
- 9એક શંકુમાં કણ $v$ ની ઝડપથી વર્તુળમય ગતિ કરે છે.તો...View Solution
- 10સ્થિર અવસ્થામાં રહેલા પદાર્થની શરૂઆતની સ્થિતિ $3 \hat{i}-8 \hat{j}$ દ્વારા આપવામાં આવે છે. તો અચળ પ્રવેગથી ગતિ કરે છે અને $4 \,s$ બાદ $2 \hat{i}+4 \hat{j}$ સુધી પહોચે છે. તેનો પ્રવેગ શું હશે?View Solution