પ્રથમ ક્રમ પ્રક્રિયાનો અદ્ય આયુ સમય $10$ મિનિટ છે. જો પ્રારંભિક મૂલ્ય $0.08$ મોલ/લીટર અને કોઈ જ ક્ષણે તેની સાંદ્રતા $0.01$ મોલ/લીટર હોય તો ...... મિનિટ થાય.
Easy
Download our app for free and get started
b
${n_t}{\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \frac{{{n_0}}}{{{2^n}}}$
${n_t}{\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \frac{{{n_0}}}{{{2^n}}}$
${2^n}{\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \frac{{{n_0}}}{{{n_1}}}{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \frac{{0.08}}{{0.01}}{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} 8$
$n{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} 3$
${\mkern 1mu} n{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} \frac{t}{{{t_{1/2}}}}{\mkern 1mu} $
$t{\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} 3{\mkern 1mu} {\mkern 1mu} \times {\mkern 1mu} {\mkern 1mu} 10{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} 30{\mkern 1mu} {\mkern 1mu} \,\min $
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનીચે પૈકી કયું વિધાન સાચું છે?
- 2પ્રથમ ક્રમની રાસાયણિક પ્રક્રિયાનો અર્ધઆયુ સમય $6.93$ મિનિટ છે. તો $99\%$ રાસાયણિક પ્રક્રિયા પૂર્ણ થવા માટે ........ મિનિટ જરૂરી છે. $(\log \,2 = 0.301)$View Solution
- 3View Solutionદ્વિતીય ક્રમની પ્રક્રિયા માટે વેગઅચળાંકનો એકમ .... થશે.
- 4$2NO_(g) + O_{2(g)} \rightarrow 2NO_{2(g)}$ પ્રક્રિયા પ્રણાલી માટે, કદ એ અચાનક ઘટીને અડધું થાય છે. જો પ્રક્રિયા એ પ્રથમ ક્રમની $O_2$ માટે અને દ્વિતીય ક્રમની $NO $ માટે હોય, તો પ્રક્રિયાનો દર.....View Solution
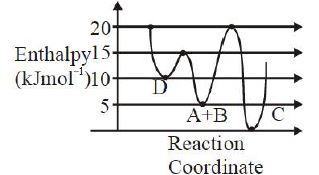
- 5$A$ અને $B$ વચ્ચેની નીચેની પ્રક્રિયાની એન્થાલ્પીનો આપેલ આલેખ ધ્યાનમાં લો. $A + B \to C + D$View Solution
ખોટું વિધાન ઓળખો.
- 6મનુષ્યનાં શરીરમાં $24$ કલાક પછી રેડીયોએક્ટિવ પદાર્થની $0.01 \mu $ ક્રિયાશીલતા જરૂરી છે. તે રેડીયોએક્ટિવનો અર્ધઆયુ $6 $ કલાક છે. તો રેડીયોએક્ટિવ પદાર્થનો મહત્તમ ક્રિયાશીલતા કેટલી દાખલ કરી શકાય?View Solution
- 7અચળ તાપમાન પ૨ વાયુ અવસ્થામાં નીચે આપેલ એક તબક્કીય પ્રક્રિયા ને ધ્યાનમાં લો.View Solution
$2 \mathrm{~A}_{(\mathrm{g})}+\mathrm{B}_{(\mathrm{g})} \rightarrow \mathrm{C}_{(\mathrm{g})}$
જ્યારે પ્રક્રિયા, $A$ નું $1.5 \mathrm{~atm}$ દબાણ અને $\mathrm{B}$ નાં $0.7 \mathrm{~atm}$ દબાણ સાથે પ્રારંભ (શરૂ) કરવામાં આવ્યો હોય ત્યારે પ્રક્રિયાનો પ્રારંભિક વેગ $r_1$ તરીક નોંધવામાં આવ્યો. થોડાક સમય પછી, જ્યારે $C$ નું દબાણ $0.5 \mathrm{~atm}$ થાય છે ત્યારે $r_2$ વેગ નોંધવામા આવ્યો, $r_1: r_2$ ગુણોત્તર ............ $\times 10^{-1}$ છે.
(નજીક નો પૂર્ણાક)
- 8પ્રક્રિયા $X \to Y$ માં પ્રક્રિયક $X$ ની સાંદ્રતા $1.5$ ગણી વધારતા પ્રક્રિયાનો વેગ $1.837$ ગણો વધે છે. તો $X$ ના સંદર્ભમાં પ્રક્રિયાનો ક્રમ જણાવો.View Solution
- 9$A + B\rightarrow C$ નીચેની પ્રક્રિયા માટે દર્શાવેલ માહિતીને લાગુ પડતુ દર નિયમ પસંદ કરો.View Solution
$1$. $[A]$ $0.012$, $[B]$ $0.0351\rightarrow $ પ્રારંભિક દર $ = 0.10$
$2$. $[A]$ $0.024$, $[B]$ $0.070\rightarrow $ પ્રારંભિક દર $= 1.6$
$3$. $[A]$ $0.024$, $[B]$ $0.035\rightarrow $ પ્રારંભિક દર $ = 0.20$
$4$. $[A]$ $0.012$ , $[B]$ $0.070\rightarrow $ પ્રારંભિક દર $ = 0.80$
- 10શૂન્ય ક્રમ પ્રક્રિયા માટે $K= 2 \times 10^{-2}$ મોલ $L^{-1}$ સેકન્ડ $^{-1}$ છે. જો $25$ સેકન્ડ પછી પ્રક્રિયકની સાંદ્રતા $0.5\,M$ થાય તો તેની પ્રારંભિક સાંદ્રતા ...... $M$ હોવી જોઈએ.View Solution