પર્વતના તળિયે અને ઉપર બેરોમીટરમાં મરકયુરીની ઊંચાઇ $75 cm$ અને $50 cm $ છે.જો મરકયુરીની અને હવાની ઘનતાનો ગુણોત્તર $10^4$ હોય ,તો પર્વતની ઊંચાઇ ....... $km$ થાય?
Diffcult
b
(b)Difference of pressure between sea level and the top of hill
\(\Delta\)P\( = ({h_1} - {h_2}) \times {\rho _{Hg}} \times g\)\( = (75 - 50) \times {10^{ - 2}} \times {\rho _{Hg}} \times g\) …\((i)\)
and pressure difference due to h meter of air
\(\Delta\)P =\(h \times {\rho _{air}} \times g\) …\((ii)\)
By equating \((i)\) and \( (ii)\) we get
\(h \times {\rho _{air}} \times g = (75 - 50) \times {10^{ - 2}} \times {\rho _{Hg}} \times g\)
\(\therefore \;h = 25 \times {10^{ - 2}}\left( {\frac{{{\rho _{Hg}}}}{{{\rho _{air}}}}} \right)\)\( = 25 \times {10^{ - 2}} \times {10^4} = 2500\,m\)
Height of the hill \(= 2.5 km.\)
(b)Difference of pressure between sea level and the top of hill
\(\Delta\)P\( = ({h_1} - {h_2}) \times {\rho _{Hg}} \times g\)\( = (75 - 50) \times {10^{ - 2}} \times {\rho _{Hg}} \times g\) …\((i)\)
and pressure difference due to h meter of air
\(\Delta\)P =\(h \times {\rho _{air}} \times g\) …\((ii)\)
By equating \((i)\) and \( (ii)\) we get
\(h \times {\rho _{air}} \times g = (75 - 50) \times {10^{ - 2}} \times {\rho _{Hg}} \times g\)
\(\therefore \;h = 25 \times {10^{ - 2}}\left( {\frac{{{\rho _{Hg}}}}{{{\rho _{air}}}}} \right)\)\( = 25 \times {10^{ - 2}} \times {10^4} = 2500\,m\)
Height of the hill \(= 2.5 km.\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionતળાવમાં તરતી બોટમાં એક લોખંડનો ટુકડો રાખેલ છે. જો આ ટુકડાને તળાવમાં નાખવામાં આવે તો પાણીનું લેવલ
- 2$1 \;\mathrm{m}$ લંબાઈ ધરાવતા એક નળાકારને એવી ધાતુમાથી બનાવેલ છે કે જેનો રેખીય પ્રસરણાંક ખૂબ નાનો છે તેને $0^{\circ} \mathrm{C}$ તાપમાને રહેલ પાણીની સપાટી ઉપર મુક્તા તેની $20\; \mathrm{cm}$ લંબાઈ સપાટીથી ઉપર રહે છે.જ્યારે પાણીનું તાપમાન વધીને $4^{\circ} \mathrm{C}$ થાય ત્યારે નળાકારની $21 \;\mathrm{cm}$ લંબાઈ સપાટીથી ઉપર રહે છે, તો $\mathrm{T}=4^{\circ} \mathrm{C}$ એ $\mathrm{T}=0^{\circ} \mathrm{C}$ ની સાપેક્ષે ઘનતા લગભગ કેટલી થાય?View Solution
- 3$1\,cm ^3$ ધનફળ ધરાવતો એક પરપોટો $40\,m$ ઊંચાઈ ધરાવતા તળાવના તળિયેથી $12^{\circ}\,C$ તાપમાનવાળી સપાટી તરફ જાય છે. અહી વાતાવરણનું દબાણ $1 \times 10^5\,Pa$ અને પાણીની ધનતા $1000\,kg / m ^3$ તથા $g =10\,m / s ^2$ છે. $40\,m$ ઊંડાઈએ પાણી અને તેની ઉપરની સપાટી વચ્યે તાપમાનનો કઈ તફાવત નથી. જ્યારે હવાનો પરપોટો સપાટી તરફ પહોંચશે ત્યારે તેનું ધનફળ $..........\,cm^3$ હશે.View Solution
- 4$0.1 \,m $ બાજુવાળી ચોરસ પ્લેટ , $0.01\, poise$ શ્યાનતા ગુણાંક ધરાવતા પ્રવાહીમાં બીજી પ્લેટ પર $0.1\, m/s$ ના વેગથી ગતિ કરે છે,જો શ્યાનતા બળ $0.002\, N$ લાગતું હોય,તો બે પ્લેટ વચ્ચેનું અંતર કેટલું હશે?View Solution
- 5એક ટાંકીમાં $20 \,^oC$ તાપમાને ભરેલા તેલમાં થઈને પતન પામતા $ 2.0\, mm$ ત્રિજ્યાના એક કૉપર. બૉલનો અંતિમ વેગ $6.5\, cm\, s^{-1}$ છે. $20 \,^oC$ તાપમાને તેલની શ્યાનતા ગણો. તેલની ઘનતા $1.5 \times 10^3\, kg\, m^{-3}$ છે, તાંબાની ઘનતા $8.9\times 10^3\,kg\,m^{-3}$ છે.View Solution
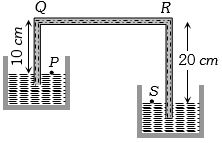
- 6પ્રવાહીની ઘનતા $ 1.5 gm/cc$ છે,તો $P$ અને $S$ બિંદુ વચ્ચે દબાણનો તફાવત કેટલો થાય?View Solution
- 7એક નાનો $m$ દળ અને $\rho$ ધનતા ધરાવતા બોલને $\rho_0$ જેટલી ધનતા ધરાવતા સિન્ગધ પ્રવાહીમાં મૂકવામાં આવે છે. અમુક સમયબાદ, બોલ અચળ વેગ સાથે પડે છે. બોલ ઉપર લાગતું સ્નિગધ (શ્યાનતા) બળ . . . .હશે.View Solution
- 8View Solutionવિધાન : પ્રવાહમાં જ્યારે દબાણ વધુ હોય ત્યાં વેગ ઓછો હોય અને ઊલટું પણ (દબાણ ઓછું અને વેગ વધુ)
કારણ : બર્નુલીના નિયમ મુજબ આદર્શ પ્રવાહીના વહન માટે એકમ દળમાં રહેલ કુલ ઉર્જા અચળ હોય.
- 9$r_1$ અને $r_2$ ત્રિજ્યા અને $l_1$ અને $l_2$ લંબાઈ ધરાવતી બે નળીને શ્રેણીમાં જોડેલ છે અને બંનેમાથી પ્રવાહ ધારારેખી વહન કરે છે. $P_1$ અને $P_2$ એ બે નળીના ચેડાં વચ્ચેનો દબાણ નો તફાવત છે.જો $P_2=4P_1$ અને $l_2= \frac{l_1}{4}$, તો ત્રિજ્યા $r_2$ કેટલી હશે?View Solution
- 10$A $ અને $B $ પદાર્થો પાણીમાં તરે છે,$A$ પદાર્થનું $\frac{1}{2}$ કદ પાણીમાં ડુબેલું અને $B $ પદાર્થનું $\frac{1}{4}$કદ પાણીની બહાર છે,તો ઘનતાનો ગુણોત્તર કેટલો થાય?View Solution
