$r_1$ અને $r_2$ ત્રિજ્યા અને $l_1$ અને $l_2$ લંબાઈ ધરાવતી બે નળીને શ્રેણીમાં જોડેલ છે અને બંનેમાથી પ્રવાહ ધારારેખી વહન કરે છે. $P_1$ અને $P_2$ એ બે નળીના ચેડાં વચ્ચેનો દબાણ નો તફાવત છે.જો $P_2=4P_1$ અને $l_2= \frac{l_1}{4}$, તો ત્રિજ્યા $r_2$ કેટલી હશે?
JEE MAIN 2017, Diffcult
d
The volume of liquid flowing through both the tubes i.e., rate of flow of liquid same.
The volume of liquid flowing through both the tubes i.e., rate of flow of liquid same.
\(Therefore,V = {V_1} = {V_2}\)
\(i.e.,\frac{{\pi {p_1}r_1^4}}{{8\eta {l_1}}} = \frac{{\pi {p_2}r_2^4}}{{8\eta {l_2}}}\)
\(or\,\,\,\,\,\,\frac{{{p_1}r_1^4}}{{{l_1}}} = \frac{{{p_2}r_2^4}}{{{l_2}}}\)
\(\,\,\,\,{P_2} = 4\,{P_1}\,\,and\,{l_2} = {l_1}/4\)
\(\frac{{{p_1}r_1^4}}{{{l_1}}} = \frac{{4{p_1}r_2^4}}{{{l_1}/4}} \Rightarrow r_2^4 = \frac{{r_1^4}}{{16}}\)
\( \Rightarrow {r_2} = {r_1}/2\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક હવાના પરપોટા (bubble)નું કદ બમણુંં થઈ જાય છે, જ્યારે તે તળાવના તળિયેથી તેની સપાટી સુધી ઉપર ઊઠે છે. વાતાવરણનું દબાણ પારાનું $75 \,cm$ છે. પારાથી તળાવના પાણીની ઘનતાનો ગુણોત્તર $\frac{40}{3}$ છે તો તળાવની ઉંચાઈ મીટરમાં કેટલી છે ?View Solution
- 2શિરોલંબ સમતલમાં એક પાતળી નળીને વાળીને $r$ ત્રિજ્યાનું વર્તુળ બનાવવામાં આવે છે.${\rho _1}$ અને ${\rho _2}\left( {{\rho _1} > {\rho _2}} \right)$ ઘનતા ધરાવતા બે સમાન કદબા એકબીજામાં મિશ્ર ના થાય તેવા પ્રવાહી દ્વારા અડધું વર્તુળ ભરેલ છે.શિરોલંબ અને બંને પ્રવાહી મળતા હોય તે સપાટી વચ્ચે વચ્ચેનો ખૂણો $\theta$ કેટલો થાય?View Solution
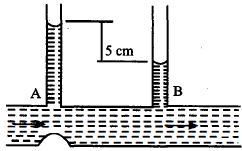
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે મેનોમીટરની બે નળી વચ્ચેનો તફાવત $5\, cm$ છે. $A$ અને $B$ નળીના આડછેડનું ક્ષેત્રફળ અનુક્રમે $6\, mm^2$ અને $10\, mm^2$ છે.તો નળીમાં પાણી ......... $ cc/s$ દરથી વહન કરતું હશે?$(g\, = 10\, ms^{-2})$View Solution
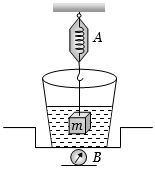
- 4એક સ્પ્રિંગકાંટો $A$ તેની સાથે લટકાવેલ બ્લોક $m$ નું અવલોકન $2\, kg$ દર્શાવે છે. જ્યારે વજનકાંટા $B$ પર મૂકેલું બીકર પ્રવાહીથી ભરવામાં આવે છે ત્યારે તે $5 \,kg $ અવલોકન દર્શાવે છે. આકૃતિ માં દર્શાવ્યા મુજબ લટકાવેલું દળ પ્રવાહીની અંદર રહે તેમ બંને વજનકાંટા ને ગોઠવેલા છે. આ પરિસ્થિતી માં .....View Solution
- 5$A $ અને $B $ પદાર્થો પાણીમાં તરે છે,$A$ પદાર્થનું $\frac{1}{2}$ કદ પાણીમાં ડુબેલું અને $B $ પદાર્થનું $\frac{1}{4}$કદ પાણીની બહાર છે,તો ઘનતાનો ગુણોત્તર કેટલો થાય?View Solution
- 6$1\,cm ^3$ ધનફળ ધરાવતો એક પરપોટો $40\,m$ ઊંચાઈ ધરાવતા તળાવના તળિયેથી $12^{\circ}\,C$ તાપમાનવાળી સપાટી તરફ જાય છે. અહી વાતાવરણનું દબાણ $1 \times 10^5\,Pa$ અને પાણીની ધનતા $1000\,kg / m ^3$ તથા $g =10\,m / s ^2$ છે. $40\,m$ ઊંડાઈએ પાણી અને તેની ઉપરની સપાટી વચ્યે તાપમાનનો કઈ તફાવત નથી. જ્યારે હવાનો પરપોટો સપાટી તરફ પહોંચશે ત્યારે તેનું ધનફળ $..........\,cm^3$ હશે.View Solution
- 7એક્ એરોપ્લેન ઉડ્યન સ્તરે અચળ ઝડપે રહેલ છે અને તેની બે પાંખોમાં દરેકનું ક્ષેત્રફળ $40 \mathrm{~m}^2$ છે. જો તેની નીચેની પાંખની સપાટી પર હવાની ઝડ૫ $180 \mathrm{~km} / \mathrm{h}$ અને ઉપરની સપાટી પર $252 \mathrm{~km} / \mathrm{h}$ હોય તો પ્લેનનું દળ_________$kg$છે. (હવાની ઘનતા $1 \mathrm{~kg} \mathrm{~m}^{-3}$ અને $10 \mathrm{~ms}^{-2}$ લો.)View Solution
- 8પાણીને સમાવતું એક નળાકાર, $H$ ઊંચાઈના ટેબલ પર રહેલો છે. નળાકારના તળિયા પરની એક બાજુ પર નાનું છિદ્ર પાડવામાં આવે છે. પાણીનો પ્રવાહ એ ટેબલથી $R$ જેટલા સમક્ષિતિજ અંતરે જમીન પર અથડાય છે. તો પછી નળાકારમાં પાણીની ઊંડાઈ કેટલી છે ?View Solution
- 9ઓરડાના તાપમાને તેલની ટાંકીમાં પડતા $5\,mm$ ત્રિજ્યાના તાંબાના બોલનો ટર્મિનલ વેગ $10\,cm-s ^{-1}$ છે. જો ઓરડાના તાપમાને તેલની સ્નિગ્ધતા $0.9\,kg\,m ^{-1}s ^{-1}$ હોય, તો શ્યાનતા બળ કેટલું હશે?View Solution
- 10$20\; m$ ની ઊંચાઈનો નળાકાર સંપૂર્ણપણે પાણીથી ભરેલો છે. તેના તળિયાની નજીક નળાકારની બાજુની દિવાલ પરના નાના છિદ્રમાંથી બહાર આવતા પાણીના પ્રવાહનો વેગ ($ m/s$ માં) કેટલો હશે?View Solution
