પૃષ્ઠ $S$ માંથી કેટલું વિદ્યુત ફલ્કસ પસાર થાય?
AIIMS 2003, Easy
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionબળના વિદ્યુત રેખાને લાગતું સાચું વિધાન પસંદ કરો.
- 2હાઇડ્રોજનમાં એક ઇલેક્ટ્રોન ન્યુક્લિયસની ફરતે $r$ ત્રિજ્યાની વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે. તે બન્ને વચ્ચે લાગતું કુલંબ બળ $\overrightarrow F $ કેટલું હશે? ($K = \frac{1}{{4\pi {\varepsilon _0}}}$)View Solution
- 3એક લાંબા પોલા નળાકારના ઉપરના અડધા ભાગમાં ઘન સપાટી વિદ્યુતભાર $\sigma $ અને નીચેના અર્ધ ભાગમાં ઋણ સપાટી-વિદ્યુતભાર $-$$\sigma $ રહેલ છે.નળાકારને ફરતે વિદ્યુતક્ષેત્ર રેખાઆકૃતિ ______ જેવી દેખાશે. (આકૃતિ રેખાકૃતિ સૂચવે છે અને તેઓ એક જ સ્કેલ પર દોરેલી નથી.)View Solution
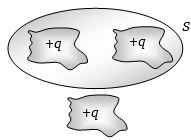
- 4એક વિદ્યુતભારીત વસ્તુ સાથે સંકળાયેલું વિદ્યુત ફલક્સ $\phi$ છે. આ પદાર્થને હવે ધાતુના પાત્રની અંદર મૂકવામાં આવ્યો છે. પાત્રની બહાર ફલક્સ $\phi$ કેટલું હશે?View Solution
- 5$ + \lambda \,C/m$ અને $ - \lambda \,C/m$ના બે સમાંતર અનંત રેખીય વિધુતભારો કે જે રેખીય વિજભાર ઘનતા ધરાવે છે તેઓને મુક્ત અવકાશમાં એક બીજાથી $2R$ અંતરે મુકેલ છે. આ બે રેખીય વિજભારની મધ્યમાં વિદ્યુતક્ષેત્ર કેટલું હશે ?View Solution
- 6જો $\vec p$ ડાઈપોલ મોમેન્ટ ધરાવતા ડાઈપોલને નિયમિત વિદ્યુતક્ષેત્ર $\vec E$ માં મુક્તા તેના પર કેટલું ટોર્ક લાગશે?View Solution
- 7અવગણ્ય કદ ધરાવતાં બે એક સરખા વીજભારિત ગોળાઓ અનુક્રમે $2.1\, nC$ અને $-0.1\, nC$ વીજભાર ધરાવે છે. બંનેને એકબીજાનાં સંપર્કમાં લાવી $0.5$ મીટર અંતર માટે જુદા પાડવામાં આવે છે. બંને ગોળાઓ વચ્ચે ઉદ્દભવતું સ્થિત વિદ્યુત બળ $.......... \, \times 10^{-9} \,N$ છે. [ $4 \pi \varepsilon_{0}=\frac{1}{9 \times 10^{9}} SI$ એકમ આપેલ છે. ]View Solution
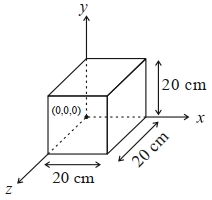
- 8વિદ્યુતક્ષેત્રને $\vec{E}=4000 x^2 \hat{i} \frac{ V }{ M }$ સમીકરણ વડે રજૂ કરેલ છે. $20\,cm$ ની બાજુ (આકૃત્તિમાં દર્શાવ્યા અનુસાર) ધરાવતા સમધનમાંથી પસાર થતું ફ્લક્સ $................V\,cm$ થશે.View Solution
- 9$R$ ત્રિજ્યા ધરાવતા ઘન ગોળની વિજભાર ઘનતા $0 \leq r \leq R$ માટે $\rho = {\rho _0}\left( {1 - \frac{r}{R}} \right)$ મુજબ આપવામાં આવે છે. તો બોલની બહાર વિદ્યુતક્ષેત્ર કેટલું હશે?View Solution
- 10કોઈ વિભાગનું વિદ્યુતક્ષેત્ર $\overrightarrow{ E }=\frac{2}{5} E _{0} \hat{ i }+\frac{3}{5} E _{0} \hat{ j }$ છે, જ્યાં $E _{0}=4.0 \times 10^{3}\, \frac{ N }{ C }$ છે. $Y - Z$ સમતલમાં $0.4 \,m ^{2}$ ક્ષેત્રફળ ધરાવતી સપાટીનું વિદ્યુતફ્લક્સ ....... $Nm ^{2} C ^{-1}$ હશે.View Solution