\(\text { Charge density, } \rho=\rho_{0}\left(1-\frac{r}{R}\right)\)
\(d q=\rho d v\)
\(q_{i n}=\int d q=\rho d v\)
\(=\rho_{0}\left(1-\frac{r}{R}\right) 4 \pi r^{2} d r \quad\left(\because d v=4 \pi \mathrm{r}^{2} \mathrm{dr}\right)\)
\(=4 \pi p_{0} \int_{0}^{R}\left(1-\frac{r}{R}\right) r^{2} d r\)
\(=4 \pi \rho_{0} \int_{0}^{R} r^{2} d r-\frac{r^{2}}{R} d r\)
\(=4 \pi \rho_{0}\left[\left[\frac{r^{3}}{3}\right]_{0}^{R}-\left[\frac{r^{4}}{4 R}\right]_{0}^{R}\right]\)
\({=4 \pi \rho_{0}\left[\frac{R^{3}}{3}-\frac{R^{4}}{4 R}\right]}\)
\({=4 \pi \rho_{0}\left[\frac{R^{3}}{3}-\frac{R^{3}}{4}\right]=4 \pi \rho_{0}\left[\frac{R^{3}}{12}\right]}\)
\({q=\frac{\pi \rho_{0} R^{3}}{3}}\)
\(E .4 \pi r^{2}=\left(\frac{\pi \rho_{0} R^{3}}{3 \epsilon_{0}}\right)\)
Electric field outside the ball, \(E=\frac{\rho_{0} R^{3}}{12 \epsilon_{0} r^{2}}\)
Download our appand get started for free
Similar Questions
- 1$q$ વિદ્યુતભાર ધરાવતા બે ધન આયનો વચ્ચેનું અંતર $d $ છે. જો તેમની વચ્ચેનું અપાકર્ષણ બળ $F $ હોય, તો દરેક આયન પર ખૂટતાં ઇલેકટ્રોનની સંખ્યા કેટલી હશે? ($e$ ઇલેક્ટ્રોન પરનો વિદ્યુતભાર છે)View Solution
- 2એક અનંત લંબાઈનો રેખીય વિદ્યુતભાર $2 \,cm$ અંતરે $9 \times 10^4 \;N/C$ વિદ્યુતક્ષેત્ર ઉત્પન્ન કરે છે. રેખીય વિદ્યુતભાર ઘનતા ($\mu C / m$ માં) ગણો.View Solution
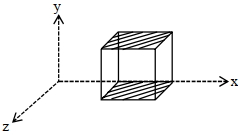
- 3એક સમઘનને $\overrightarrow{{E}}=150\, {y}^{2}\, \hat{{j}}$ જેટલા વિદ્યુતક્ષેત્રની અંદર મૂકવામાં આવે છે. સમઘનની બાજુની લંબાઈ $0.5 \,{m}$ અને તેને આકૃતિમાં દર્શાવ્યા પ્રમાણે મૂકવામાં આવે છે. સમઘનની અંદરનો વિદ્યુતભાર $(\times 10^{-11} {C}$ માં) કેટલો હશે?View Solution
- 4એક વિદ્યુત ડાયપોલ, $2 \,cm$ અંતરે દૂર $1 \,\mu C$ માત્રાના બે વિરૂધ્ધ વિદ્યુતભારોની બનેલી છે. આ ડાયપોલને $10^5\,N/C$ ના બાહ્ય ક્ષેત્રમાં મૂકવામાં આવી છે. ડાયપોલ પર લાગતું મહત્તમ ટોર્ક .......... $Nm$View Solution
- 5$5\,\mu C$ બિંદુવત વિજભારથી $80\, cm$ અંતરે વિદ્યુતક્ષેત્રની પ્રબળતા કેટલી હશે?View Solution
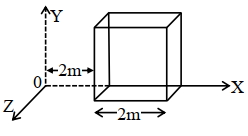
- 6અવકાશમાં $\vec{E}=(2 x \hat{i}) N C^{-1}$ જેટલું વિદ્યુતક્ષેત્ર પ્રવર્ત છે. નીચે દર્શાવેલ આકૃતિ મુજબ $2 \mathrm{~m}$ બાજુ ધરાવતો સમધન આ વિસ્તારમાં મૂકવામાં આવે છે : સમધનમાંથી પસાર થતું ફ્લકસ ........... $\mathrm{Nm}^2 / \mathrm{C}$ હશે.View Solution
- 7ઉગમબિંદુ $(0,0,0)$ આગળ રહેલ એક વિદ્યુત ડાયપોલની ડાયપોલ મોમેન્ટ $\overrightarrow{\mathrm{p}}=(-\hat{\mathrm{i}}-3 \hat{\mathrm{j}}+2 \hat{\mathrm{k}}) \times 10^{-29}\; \mathrm{C} \cdot \mathrm{m}$ છે.ડાયપોલને કારણે $\overrightarrow{\mathrm{r}}=+\hat{\mathrm{i}}+3 \hat{\mathrm{j}}+5 \hat{\mathrm{k}}$ આગળ રહેલ વિદ્યુતક્ષેત્ર કોને સમાંતર હોય? ($\overrightarrow{\mathrm{r}} \cdot \overrightarrow{\mathrm{p}}=0)$View Solution
- 8$\overrightarrow{\mathrm{E}}=\frac{2 \hat{i}+6 \hat{j}+8 \hat{k}}{\sqrt{6}}$ થી રજૂ થતું વિદ્યુતક્ષેત્ર $4 \mathrm{~m}^2$ ક્ષેત્રફળ અને $\hat{n}=\left(\frac{2 \hat{i}+\hat{j}+\hat{k}}{\sqrt{6}}\right)$ જેટલો એકમ સદિશ ધરાવતી સપાટીમાંથી પસાર થાય છે. સપાટી સાથે સંકળાયેલ વિદ્યુત ફ્લક્સ. . . . . .$Vm$ હશે.View Solution
- 9$1$ કુલંબના બે વિદ્યુતભારોને $1 \,km$ દૂર મૂકવામાં આવે, તો તેમની વચ્ચે લાગતું બળ ............. $N$ હશે.View Solution
- 10એક ધન ધાતુના ગોળા પાસે $+ 3Q$ વિદ્યુતભાર છે. જે $-Q$ વિદ્યુતભાર વાળા સુવાહક ગોળીય કવચને સમકેન્દ્રિત છે. ગોળાની ત્રિજ્યા $a$ અને ગોળીય કવચની $b$ છે. $(b > a)$. કેન્દ્રથી $R$ અંતર આગળ $(a < R < b) \,f$ વિદ્યુતક્ષેત્ર ....... છે.View Solution
