પૃથ્વીની $axis$ આગળ ત્રિજ્યા $R$ છે અને તે તેના ભ્રમણનો વેગ એવા મૂલ્ય સુધી વધારે છે જ્યારે $60^{\circ}$ ના અક્ષાંક્ષખૂણે ઉભેલો માણસ વજનરહિત અનુભવે. આવા કિસ્સામાં દિવસનો સમયગાળો $........$
Medium
Download our app for free and get started
c
(c)
(c)
\(0=g-R \omega ^2 \cos ^2 60^{\circ}\)
\(\omega ^2=\frac{4 g}{R}\)
\(\omega ^2=2 \sqrt{\frac{g}{R}}\)
\(\frac{2 \pi}{T}=2 \sqrt{\frac{g}{R}}\)
\(T=\pi \sqrt{\frac{R}{g}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો $V$ એ ગોળાની સમાન ધનતાને લીધે તેની સપાટી પરનો ગુરુત્વીય વિભવ હોય તો, ગોળાના કેન્દ્રમાં તેનું મૂલ્ય ....... હશે.View Solution
- 2એકબીજા પરના ગુરુત્વાકર્ષણના કારણે $1\, {kg}$ દળના બે સમાન કણો $R$ ત્રિજયાના વર્તુળમાં ભ્રમણ કરે છે. તો દરેક કણની કોણીય ઝડપ ..... થશે.View Solution
- 3View Solutionજો ગુરુત્વાકર્ષણનો અચળાંક સમય સાથે ઘટતો હોય તો ઉપગ્રહ માટે નીચેનામાથી શું બદલાય નહીં ?
- 4View Solutionપૃથ્વી સૂર્યની આજુબાજુ ભ્રમણ કરે છે,તો કયાં બિંદુએ પૃથ્વીનો વેગ મહત્તમ થશે?
- 5$m$ દળનો માણસ એ $M$ દળ અને $R$ ત્રિજ્યાના ગ્રહ તરફ પડે છે. તે સપાટીની નજીક પહોંચે છે ત્યારે જાણો છે કે તે ગ્રહના નાના હોલમાંથી પસાર થઈ જશે. જેવો તે તેમાં પ્રેવેશે છે તે જોવે છે કે તે ગ્રહ એ $2 M / 3$ જેટલા દળ અને બિંદુવત દળ $M / 3$ ના અવગણ્ય જાડાઈના બે ગોળાકાર જોડકા વડે બનેલો છે. તો માણસ દ્વારા અનુભવાતો ગુરુત્વકર્ષી બળનો તફાવત કેટલો હશે?View Solution
- 6પૃથ્વી કેટલી કોણીય વેગ થી ફરવી જોઈએ કે $60^o$ અક્ષાંશ પર તેનો ગુરુત્વ પ્રવેગ શૂન્ય થાય?View Solution
- 7View Solutionજ્યારે પદાર્થ ને વિષુવવૃત થી ધ્રુવ પર લઈ જતા તેનું વજન
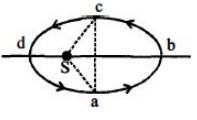
- 8આકૃતિમાં સૂર્ય $S$ ની ફરતે $abcd$ ઉપવલયાકાર કક્ષામાં ભ્રમણ કરતાં ગ્રહ માટે ત્રિકોણ $csa$ નું ક્ષેત્રફળ ઉપવલયના ક્ષેત્રફળ કરતાં $\frac {1}{4}$ ગણું છે જ્યાં $db$ એ પ્રધાન અક્ષ અને $ca$ એ ગૌણ અક્ષ છે.જો $t_1$ એ $abc$ જવા માટેનો સમય અને $t_2$ એ $cda$ માટેનો સમય હોય તો ...View Solution
- 9એ ગ્રહની આસપાસ પરિભ્રમણ કરતાં કૃત્રિમ ઉપગ્રહ માટે ગુરૂત્વાકર્ષણ બળ $(F)$ એ તેના કેન્દ્રથી $r$ અંતરે $F \propto r^2$ મૂજબ બદલાય છે. જો તેની કક્ષીય ઝડપ $v_0$ હોય તો....View Solution
- 10જો પૃથ્વીની ત્રિજ્યા $0.1\%$ જેટલી સંકોચાઈ જાય, તેનું દળ સમાન જળવાઈ રહે તો, પૃથ્વીની સપાટી પર પદાર્થનું વજન ($\%$ માં) કેટલું વધશે ?View Solution