$q$ વિદ્યુતભાર ધરાવતા બે ધન આયનો વચ્ચેનું અંતર $d $ છે. જો તેમની વચ્ચેનું અપાકર્ષણ બળ $F $ હોય, તો દરેક આયન પર ખૂટતાં ઇલેકટ્રોનની સંખ્યા કેટલી હશે? ($e$ ઇલેક્ટ્રોન પરનો વિદ્યુતભાર છે)
AIPMT 2010, Diffcult
c
According to Coulomb's law, the force of repulsion between the two positive ions each of charge \(q\) separated by a distance \(d\) is given by
According to Coulomb's law, the force of repulsion between the two positive ions each of charge \(q\) separated by a distance \(d\) is given by
\(F =\frac{1}{4 \pi \varepsilon_{0}} \frac{(q)(q)}{d^{2}} \)
\(F =\frac{q^{2}}{4 \pi \varepsilon_{0} d^{2}}\)
\(q^{2} =4 \pi \varepsilon_{0} F d^{2} \)
\(q =\sqrt{4 \pi \varepsilon_{0} F d^{2}}..........(i)\)
Since, \(q=ne\)
where,
\(n=\) number of electrons missing from each ion
\(e=\) magnitude of charge on electron
\(\therefore n = \frac{q}{e}\)
\(n = \frac{{\sqrt {4\pi {\varepsilon _0}F{d^2}} }}{e}\) (Using \((i)\))
\(=\sqrt{\frac{4 \pi \varepsilon_{0} F d^{2}}{e^{2}}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે વિદ્યુતભાર $-Q$ અને $2Q$ ને $R$ અંતરે મૂકેલા છે,તો વિદ્યુતક્ષેત્ર શૂન્ય ક્યાં થાય?View Solution
- 2$ + \sigma $ અને $ - \sigma $ પૃષ્ઠ વિધુતભાર ઘનતા ધરાવતા અનંત લંબાઈના સમતલને સૂક્ષ્મ અંતરે સમાંતર મૂકેલા છે બંને પ્લેટ વચ્ચે શૂન્યઅવકાશ છે જો ${\varepsilon _0}$ એ શૂન્યાવકાશની પરમિટિવિટી હોય તો બે પ્લેટ વચ્ચેના અવકાશમાં વિધુતક્ષેત્ર .............. મળેView Solution
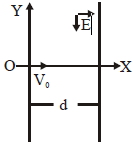
- 3એક વિજભારિત કણ ($m$ દળ અને $q$ વિજભાર) $X$ અક્ષ દિશામાં $V _{0}$ વેગથી ગતિ કરે છે.જ્યારે તે ઉગમબિંદુ પાસેથી પસાર થાય ત્યારે તે $\overrightarrow{ E }=- E \hat{ j }$ જેટલા એકસમાન વિદ્યુતક્ષેત્રમાં (જે $x = d$ સુધી પ્રવર્તે છે) દાખલ થાય છે. $x > d$ ક્ષેત્રમાં ઇલેક્ટ્રોનના ગતિપથનું સમીકરણ શું હશે?View Solution
- 4ધારો કે સમાન વિદ્યુતભારિત દિવાલ $2 \times 10^4 \mathrm{~N} / \mathrm{C}$ મૂલ્યનું એક લંબ સમાન વિદ્યુતક્ષેત્ર આપે છે. એક $2 \mathrm{~g}$ દળના વિદ્યુતભારિત કણને $20 \mathrm{~cm}$ લંબાઈના સિલ્કના દોરા વડે લટકાવવામાં આવે છે અને તે દિવાલ થી $10 \mathrm{~cm}$ દૂર રહે છે. કણ પરનો વિદ્યુતભાર $\frac{1}{\sqrt{x}}$ $\mu \mathrm{C}$ હોયતો $x$=__________થશે. $[g=10 m/s$View Solution
- 5$2 L \times 2 L \times L$ પરિણામાણ ધરાવતા લંબધનમાં $4 L ^2$ ક્ષેત્રફળ ધરાવતા પૃષ્ઠ $s$ ના કેન્દ્રસ્થાને વિદ્યુતભાર $q$ મૂકવામાં આવે તો $s$ ના સામેના પૃષ્ઠમાંથી પસાર થતું ફલફસView Solution
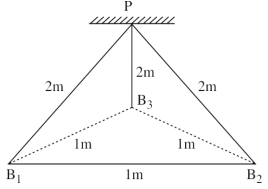
- 6ત્રણ દરેક $2 \,C$ જેટલા વિદ્યુતભારીત બોલને $2 \,m$ લંબાઈના સ્લિકના દોરાથી (આકૃતિમાં દર્શાવ્યા અનુસાર) સમાન બિંદુ $P$ આગળથી લટકાવવામાં આવ્યા છે. તેઓ $1 \,m$ બાજુનો સમબાજુ ત્રિકોણ બનાવે છે. વિદ્યુતભારીત બોલ પર લાગતુ કુલ બળ અને કોઇપણ બે વિદ્યુતભારો વચ્યે પ્રવર્તતા બળોનો ગુણોત્તર .......... થશે.View Solution
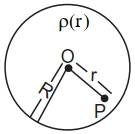
- 7$\rho(r)=\left\{\begin{array}{ll}\rho_{0}\left(\frac{3}{4}-\frac{r}{R}\right) & \text { for } r \leq R \\ \text { Zero } & \text { for } r>R\end{array}\right.$View Solution
અનુસાર બદલાતી ગોલીય સંમિત વિદ્યુતભાર વહેંચણી વિચારો,જ્યાં $r ( r < R )$ એ કેન્દ્રથી અંતર છે (આકૃતિ જુઓ) $P$ બિંદુ આગળ વિદ્યુતક્ષેત્ર $......$ હશે.
- 8એક ચોકકસ વિસ્તારમાં વિદ્યુતક્ષેત્ર $ E=Ar$ છે અને તે ત્રિજયાવર્તી દિશામાં બહાર તરફ છે. $a$ ત્રિજયાના ગોળાના કેન્દ્ર પર રહેલા વિદ્યુતક્ષેત્રથી ગોળા પર કેટલો વિદ્યુતભાર મળે?View Solution
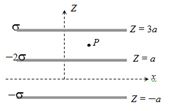
- 9આકૃતીમાં દર્શાવ્યા મુજબ ત્રણ અનંત લંબાઇથી પ્લેટોને મુકેલ છે તો $P$ બિંદુ આગળ વિદ્યુત ક્ષેત્ર....View Solution
- 10View Solutionડાઈપોલની અક્ષ આગળ અને વિષુવ રેખા પર વિદ્યુતક્ષેત્રનો ગુણોત્તર ...... હશે.
