$Q$ વિદ્યુતભાર ધરાવતા એક ધન વાહક ગોળોએ અવિદ્યુતભારીત સમકેન્દ્રિય વાહક ગોળીય કવચની આજુબાજુ આવેલો છે. ધન ગોળીય પૃષ્ઠ અને કવચની બહારના પૃષ્ઠ વચ્ચેનો સ્થિતિમાનનો તફાવત $V$ લો. જો કવચનો વિદ્યુતભાર $-3Q$ હોય તો આ બે સમાન પૃષ્ઠો સ્થિતિમાનનો નવો તફાવત .........$V$ છે.
IIT 1989, Diffcult
a
(a) In case of a charged conducting sphere
\({V_{{\rm{inside}}}} = {V_{{\rm{centre }}}} = {V_{{\rm{surface}}}} = \frac{1}{{4\pi {\varepsilon _o}}}.\frac{q}{R}\), \({V_{{\rm{outside}}}} = \frac{1}{{4\pi {\varepsilon _0}}}.\frac{q}{r}\)
If \(a\) and \(b\) are the radii of sphere and spherical shell respectively, then potential at their surface will be
\({V_{{\rm{sphere }}}} = \frac{1}{{4\pi {\varepsilon _0}}}.\frac{Q}{a}\) and \({V_{{\rm{shell}}}} = \frac{1}{{4\pi {\varepsilon _0}}}.\frac{Q}{b}\)
\(\therefore \)\(V = {V_{{\rm{sphere }}}} - {V_{{\rm{shell}}}} = \frac{1}{{4\pi {\varepsilon _0}}}.\left[ {\frac{Q}{a} - \frac{Q}{b}} \right]\)
Now when the shell is given charge \((-3Q)\), then the potential will be
\(V{'_{{\rm{sphere}}}} = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{Q}{a} + \frac{{( - 3Q)}}{b}} \right],\)\(V{'_{{\rm{shell}}}} = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{Q}{b} + \frac{{( - 3Q)}}{b}} \right]\)
\(\therefore \)\(V{'_{{\rm{sphere }}}} - V{'_{{\rm{shell}}}} = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{Q}{a} - \frac{Q}{b}} \right] = V\)
(a) In case of a charged conducting sphere
\({V_{{\rm{inside}}}} = {V_{{\rm{centre }}}} = {V_{{\rm{surface}}}} = \frac{1}{{4\pi {\varepsilon _o}}}.\frac{q}{R}\), \({V_{{\rm{outside}}}} = \frac{1}{{4\pi {\varepsilon _0}}}.\frac{q}{r}\)
If \(a\) and \(b\) are the radii of sphere and spherical shell respectively, then potential at their surface will be
\({V_{{\rm{sphere }}}} = \frac{1}{{4\pi {\varepsilon _0}}}.\frac{Q}{a}\) and \({V_{{\rm{shell}}}} = \frac{1}{{4\pi {\varepsilon _0}}}.\frac{Q}{b}\)
\(\therefore \)\(V = {V_{{\rm{sphere }}}} - {V_{{\rm{shell}}}} = \frac{1}{{4\pi {\varepsilon _0}}}.\left[ {\frac{Q}{a} - \frac{Q}{b}} \right]\)
Now when the shell is given charge \((-3Q)\), then the potential will be
\(V{'_{{\rm{sphere}}}} = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{Q}{a} + \frac{{( - 3Q)}}{b}} \right],\)\(V{'_{{\rm{shell}}}} = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{Q}{b} + \frac{{( - 3Q)}}{b}} \right]\)
\(\therefore \)\(V{'_{{\rm{sphere }}}} - V{'_{{\rm{shell}}}} = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{Q}{a} - \frac{Q}{b}} \right] = V\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
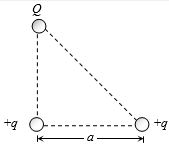
- 1સમદ્વિબાજુ કાટકોણ ત્રિકોણનાં શિરોબિંદુઓ પર $Q$, $+q$ અને $+q$ વિદ્યુતભારો આકૃતિ મુજબ મૂકેલ છે.જો સમગ્ર તંત્રની કુલ વિદ્યુતસ્થિતિઊર્જા શૂન્ય હોય,તો $Q$ = __________.View Solution
- 2$1\, g$ દળ તથા $10^{-8}\ C$ વિદ્યુતભાર ધરાવતો બોલ $600\, volt$ વિદ્યુત સ્થીતીમાન ધરાવતા બિંદુ $A$ થી શુન્ય $(0) \,volt$ વિદ્યુતસ્થીતીમાન ધરાવતા બિંદુ $B$ પર જાય છે. બિંદુ $B$ આગળ બોલનો વેગ $20\,cm/s$ છે તો બિંદુ $A$ આગળ બોલનો વેગ......$cm/s$View Solution
- 3View Solutionશા માટે કોઈ ધાતુનો કેપેસિટરમાં ડાઈ-ઈલેકટ્રીક તરીકે ઉપયોગ કરી શકાતો નથી ?
- 4કેપેસિટરને $V$ વૉલ્ટની બેટરી સાથે જોડેલ છે,તેના ડાઇઇલેક્ટ્રીક અચળાંક $k$ ધરાવતું માધ્યમ કેપેસીટરમાં દાખલ કરતાં કેપેસિટરમાં દાખલ કરતા કેપેસિટર પર નવો વિદ્યુતભાર .....View Solution
- 5$C = 10\ \mu \,F$ કેપેસિટન્સ ઘરાવતો કેપેસિટરને $12\ V$ બેટરી સાથે જોડેલ છે.ડાયઇલેકટ્રીક અચળાંક $5$ ઘરાવતી ડાયઇલેકટ્રીકને વચ્ચે મૂકતા બેટરીમાંથી કેપેસિટર પર વઘારાનો કેટલા ......$\mu \,C$ વિધુતભાર જશે?View Solution
- 6દરેક $1$ $\mu$$F$ મૂલ્ય ધરાવતા ત્રણ કેપેસિટરોને એવી રીતે જોડવામાં આવે છે, કે જેથી પરિણામી કેપેસિટન્સ $1.5$ $\mu$$F$ છે, તો....View Solution
- 7ધારોકે $C$ એ $R$ અવરોધ દ્વારા ડિસ્ચાર્જ થતા કેપેસીટરનું કેપેસીટન્સ છે ધારોકે કેપેસીટરની શરૂઆતની ઊર્જા કરતા અડધી ઊર્જા થતા લાગતો સમય $t_1$ તથા $t_2$ એ તેની પ્રારંભીક ઊર્જા કરતા ચોથા ભાગની ઊર્જા થવા માટે લાગતો સમય છે તો ગુણોત્તર $t_1/t_2$ = ….View Solution
- 8નીચે બે વિધાનો આપેલા છે. એકને કથન $(A)$ અને બીભને કારણ $(R)$ થી દર્શાવામાં આવે છે.View Solution
કથન $(A)$: સમસ્થિતિમાન પૃષ્ઠ પરથી ધન વિદ્યુતભારને દૂર કરવા કરવું પડતું કાર્ય શૂન્ય હોય છે.
કારણ $(R)$: વિદ્યુત બળ રેખાઓ સમસ્થિતિમાન પૃષ્ઠે હંમેશા લંબ હોય છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં, નીચે આપેલા વિકલપોમાંથી સૌથી યોગ્ય ઉત્તર પસંદ કરો.
- 9$50\, \mu F$ ધરાવતા કેપેસિટરને $100\, V$ ચાર્જ કરેલ છે.બેટરી દૂર કરીને બે પ્લેટ વચ્ચેનું અંતર બમણું કરવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 10બે પ્લેટો એકબીજાથી $20\, cm$ દૂર છે. તેમની વચ્ચે વિદ્યુુત સ્થિતિમાનનો તફાવત $10\, volt$ છે, તો બે પ્લેટો વચ્ચે વિદ્યુતક્ષેત્ર ......$Vm^{-1}$View Solution
