$Q$ વિજભાર બે સમકેન્દ્રિય $r$ અને $R ( R > r)$ ત્રિજ્યા ધરાવતા પોલા ગોળા પર એવી રીતે પથરાયેલ છે કે જેથી બંને ગોળા પરની પૃષ્ઠ વિજભાર ઘનતા સમાન રહે. બંનેના સમાન કેન્દ્ર આગળ વિદ્યુતસ્થિતિમાન કેટલું મળે?
AIEEE 2012,IIT 1981,JEE MAIN 2020, Diffcult
c
Let \(q_{1}\) and \(q_{2}\) be charge on two spheres of radius \('r'\) and \('R'\) respectively As, \(q_{1}+q_{2}=Q\)
Let \(q_{1}\) and \(q_{2}\) be charge on two spheres of radius \('r'\) and \('R'\) respectively As, \(q_{1}+q_{2}=Q\)
and \(\sigma_{1}=\sigma_{2} \quad\) [Surface charge density are cqual \(]\)
\(\therefore \frac{q_{1}}{r \pi r^{2}}=\frac{q_{2}}{4 \pi R^{2}}\)
So, \(q_{1}=\frac{Q r^{2}}{R^{2}+r^{2}}\) and \(q_{2}=\frac{Q R^{2}}{R^{2}+r^{2}}\)
Now, potential, \(V=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{q_{1}}{r}+\frac{q_{2}}{R}\right]\)
\(=\frac{1}{4 \pi \varepsilon_{0}}\left[\frac{Q r}{R^{2}+r^{2}}+\frac{Q R}{R^{2}+r^{2}}\right]\)
\(=\frac{Q(R+r)}{R^{2}+r^{2}} \frac{1}{4 \pi \varepsilon_{0}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$2 \times 10^{-2}\,C$ નો એક બિંદુવત વિદ્યુતભાર $P$ થી $S$ સુધી ધન $x-$ અક્ષની દિશામાં પ્રવર્તતા $30\,NC ^{-1}$ જેટલા નિયમિત વિદ્યુતક્ષેત્રમાં ગતિ કરે છે. જો $P$ અને $S$ના યામો અનુક્રમે $(1,2,0),(2,0,0),(1,-2,0)$ અને $(0,0,0)$ હોય, તો આ પ્રક્રિયામાં થતું કાર્ય $.........\,mJ$ થશે.View Solution
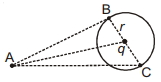
- 2$r$ ત્રિજ્યાવાળા વર્તુળના કેન્દ્ર પર $q$ જેટલો ચાર્જ રાખેલ છે, $B$ અને $C$ બિંદુઓ આ વર્તુંળના પરિઘ પર છે. જ્યારે બિંદુ $A$ આ વર્તુળથી બહાર છે. જો $W_{A B}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $B$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે અને $W_{A C}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $C$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે તો આપેલી આકૃતિ માટે કયું વિધાન સત્ય છે ?View Solution
- 3બે બિંદુઓ $P$ અને $Q$ આગળ વિદ્યુતસ્થિતિમાનમાં મૂલ્યો અનુક્રમે $10\; V$ અને $-4 \;V$ છે. તો $100$ ઈલેક્ટ્રોનને બિંદુ $P$ થી $Q$ પર લાવવા માટે કેટલું કાર્ય કરવું પડે?View Solution
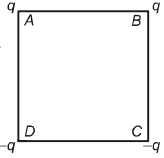
- 4આકૃતિમાં દર્શાવ્યા મુજબ ચોરસનાં શિરોબિંદુઓ પર વિદ્યુતભાર મૂકેલા છે.આ ચોરસના કેન્દ્ર પર વિદ્યુતક્ષેત્ર $\vec E$ અને વિદ્યુતસ્થિતિમાન $V$ છે.જો $A$ અને $B$ પરના વિદ્યુતભારને $D$ અને $C$ સ્થાને રહેલા વિદ્યુતભાર સાથે અદલા-બદલી કરવામાં આવે, તો ચોરસના કેન્દ્ર પર .......View Solution
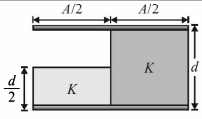
- 5એક સમાંતર પ્લેટ કેપેસિટર જેનું ક્ષેત્રફળ $A$ છે. પ્લેટ અંતર '$d$', તેને બે ડાયઈલેક્ટ્રિકમાં ભરવામાં આવે છે. આ તંત્રનું કેપેસિન્ટન્સ શું હશે ?View Solution
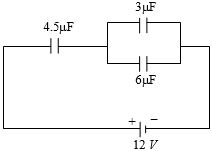
- 6આપેલ તંત્રમાં $4.5\ \mu\ F$ વચ્ચે વિધુતસ્થિતિમાનનો તફાવત કેટલા .....$V$ થાય?View Solution
- 7જો $V$ વોલ્ટના ઉદગમ સાથે $n$ કેપેસિટરો સમાંતરમાં જોડેલા હોય, તો સંગ્રહિત ઊર્જા બરાબર ........View Solution
- 8$r$ ત્રિજ્યા તથા $q$ વિદ્યુતભાર ધરાવતા મરક્યુરીના $64$ નાના ટીપા ભેગા થઇને એક મોટુ બુંદ બનાવે છે તો દરેક નાના ટીપાનો તથા મોટા બુંદની પૃષ્ટ વિદ્યુતભારનો ગુણોત્તર....View Solution
- 9જો કોઇ વિસ્તારમાં વિદ્યુત વિભવ ( વોલ્ટમાં ) $V (x,y,z) =6xy-y+2yz $ દ્રારા દર્શાવવામાં આવે તો $(1,1,0)$ બિંદુ પર વિદ્યુતક્ષેત્ર ______ $N/C$View Solution
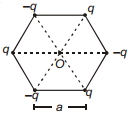
- 10નિયમિત ષટ્કોષનાં શિરોબિંદુઓ પર બિંદુુવત્ વિદ્યુતભારને આકૃતિમાં દર્શાવ્યા મુજબ રાખેલ છે. $O$ ઉગમબિંદુએ $E$ વિદ્યુતક્ષેત્ર દર્શાવતું હોય અને $V$ વિદ્યુત સ્થિતિમાન દર્શાવે છે, તોView Solution