${q_1} = 2\,\mu C$ અને ${q_2} = - 1\,\mu C$ ને $x = 0$ અને $x = 6$ પર મુકતાં વિદ્યુતસ્થિતિમાન શૂન્ય કયાં બિંદુએ થાય?
Diffcult
c
(c) Potential will be zero at two points
At internal point \((M)\) :\(\frac{1}{{4\pi {\varepsilon _0}}} \times \left[ {\frac{{2 \times {{10}^{ - 6}}}}{{(6 - l)}} + \frac{{( - 1 \times {{10}^{ - 6}})}}{l}} \right] = 0\)
\(==>\) \(l = 2\)
So distance of \(M\) from origin; \(x = 6 -2 = 4\)
At exterior point \((N)\) :\(\frac{1}{{4\pi {\varepsilon _0}}}\) \(×\) \(\left[ {\frac{{2 \times {{10}^{ - 6}}}}{{6 - l'}} + \frac{{ - 1 \times {{10}^{ - 6}}}}{{l'}}} \right] =0 \)
(c) Potential will be zero at two points
At internal point \((M)\) :\(\frac{1}{{4\pi {\varepsilon _0}}} \times \left[ {\frac{{2 \times {{10}^{ - 6}}}}{{(6 - l)}} + \frac{{( - 1 \times {{10}^{ - 6}})}}{l}} \right] = 0\)
\(==>\) \(l = 2\)
So distance of \(M\) from origin; \(x = 6 -2 = 4\)
At exterior point \((N)\) :\(\frac{1}{{4\pi {\varepsilon _0}}}\) \(×\) \(\left[ {\frac{{2 \times {{10}^{ - 6}}}}{{6 - l'}} + \frac{{ - 1 \times {{10}^{ - 6}}}}{{l'}}} \right] =0 \)
\(l'=6\)
So distance of \(N\) from origin, \(x = 6 + 6 = 12\)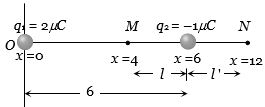
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$K$ જેટલો ડાયઈલેકિટ્રક અચળાંક ધરાવતા દ્રવ્યના બનેલા એક યોસલાને, સમાંતર પ્લટો ધરાવતા સંધારકની પ્લેટો જેટલું જ ક્ષેત્રફળ છે, અને તેની જાડાઈ $\frac{3}{4}$ d, જેટલી છે, જયાં $d$ એ પ્લેટો વચ્ચેનું અંતર છે. જ્યારે પ્લેટોની વચ્ચે યોસલાને દાખલ કરવામાં આવશે ત્યારે સંધારકતા કેટલી થશે ? ( $C _0=$ જયારે સંધારકની પ્લેટો વચ્યેનું માધ્યમ હવા હોય, ત્યાર ની સંધારકતા.)View Solution
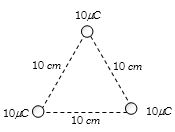
- 2આપેલ તંત્રની કુલ વિદ્યુતસ્થિતિઊર્જા કેટલા .......$J$ થાય? ( $\frac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}\ N - {m^2}/{C^2})$View Solution
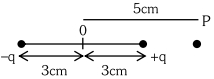
- 3બે બિંદુઓ $P$ અને $Q$ પાસે વિદ્યુતસ્થિતિમાનો અનુક્રમે $10\ V$ અને $-4\ V$ છે તો $100$ ઈલેક્ટ્રોનને $P$ થી $Q$ પર લઈ જવા કરવું પડતું કાર્ય ........View Solution
- 4$\alpha - $કણ $70\ V$ થી $50\ V$ વોલ્ટેજ ધરાવતાં બિંદુ પર જતાં ગતિઊર્જા કેટલી થાય?View Solution
- 5View Solutionહાઇડ્રોજન અયન અને એક આયનીય હીલિયમ અણુને સ્થિર સ્થિતિમાંથી સમાન વિદ્યુતસ્થિતિમાનના તફાવતથી પ્રવેગિત કરવામાં આવે છે, તો હાઇડ્રોજન અને હીલિયમની અંતિમ ઝડપનો ગુણોત્તર લગભગ કેટલો હશે?
- 6સમાંતર પ્લેટ કેપેસીટરની પ્લેટો વચ્ચેનું અંતર $2\ mm$ છે તથા તેને $300\, V$ ની બેટર વડે જોડીને વિદ્યુતભારીત કરેલ છે તો ઊર્જા ઘનતા....$J/m^3$View Solution
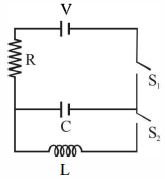
- 7નીચે દર્શાવેલ આકૃતિ મુજબ પ્રારંભમાં બંને કળ ખુલ્લી રાખેલ છે.હવે કળ $S1$ ને બંઘ કરવામાં આવે છે.પણ $S2$ ઓપન છે.( અત્રે કેપેસિટર પર $q$ ચાર્જ છે.$\tau $ $=RC$ કેપેસિટિવ અચળાંક છે.) નીચેના વિકલ્પો પૈકી કયું વિધાન સત્ય છે.?View Solution
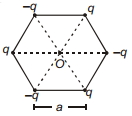
- 8નિયમિત ષટ્કોષનાં શિરોબિંદુઓ પર બિંદુુવત્ વિદ્યુતભારને આકૃતિમાં દર્શાવ્યા મુજબ રાખેલ છે. $O$ ઉગમબિંદુએ $E$ વિદ્યુતક્ષેત્ર દર્શાવતું હોય અને $V$ વિદ્યુત સ્થિતિમાન દર્શાવે છે, તોView Solution
- 9બે એક સરખા કેપેસીટર સમાન કેપેસીટન્સ (સંધારકતા) ધરાવે છે. તેમાનાં એકને $V$ સ્થિતિમાન વડે અને બીજાને $2 V$ સ્થિતિમાન વડે વીજભારિત કરવામાં આવે છે. બંનેના ઋણ છેડાને જોડેલા છે જયારે તેમના ધન છેડાઓને પણ જોડવામાં આવે ત્યારે સંયુક્ત તંત્રની ઊર્જામાં થતો ઘટાડો______છે.View Solution
- 10આકૃતિમાં એક વિદ્યુત દ્રી-ધ્રુવી દર્શાવેલો છે. આ દ્વિ-ધ્રુવીને લીધે બિંદુ $P$ આગળ વિદ્યુત સ્થિતિમાન $........\times 10^2\,V$ છે.$\left(\epsilon_0=\right.$ મુક્ત અવકાશનો પરાવૈદ્યુતાંક અને $\left.\frac{1}{4 \pi \epsilon_0}=K\right)$ :View Solution