Magnetic field induction due to vertical loop at the centre \(O\) is
\(B_{1}=\frac{\mu_{0} I}{2 R}\)
It acts in horizontal direction.
Magnetic field induction due to horizontal loop at the centre \(O\) is
\(B_{2}=\frac{\mu_{0} 2 I}{2 R}\)
It acts in vertically upward direction.
As \(B_{1}\) and \(B_{2}\) are perpendicular to each other, therefore the resultant magnetic field induction at the centre \(O\) is
\({B_{\text {net }}=\sqrt{B_{1}^{2}+B_{2}^{2}}=\sqrt{\left(\frac{\mu_{0} I}{2 R}\right)^{2}+\left(\frac{\mu_{0} 2 I}{2 R}\right)^{2}}}\)
\({B_{\text {net }}=\frac{\mu_{0} I}{2 R} \sqrt{(1)^{2}+(2)^{2}}=\frac{\sqrt{5} \mu_{0} I}{2 R}}\)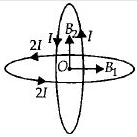
Download our appand get started for free
Similar Questions
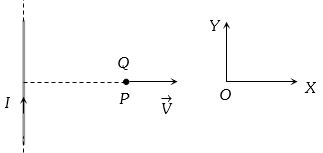
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે અતિ લાંબા સુરેખ વાહક તારમાં $I$ જેટલો વિદ્યુતપ્રવાહ વહે છે. કોઈ એક ક્ષણે $P$ બિંદુ પાસે $+q$ વિદ્યુતભારનો વેગ $\vec v$ ધન $X$ દિશામાં છે, તો વિદ્યુતભાર પર લાગતું બળ કઈ દિશામાં હશે?View Solution
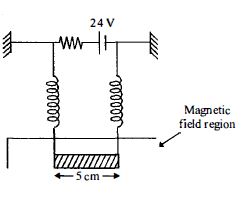
- 2આકૃતિમાં દર્શાવેલ પરિપથમાં ઉપર અને નીચે તાર અને જમણી અને ડાબી બાજુએ સમાન સ્પ્રિંગ છે. નીચેના તારનું દળ $10\, g$ અને લંબાઈ $5\, cm$ છે. તારના વજનને કારણે સ્પ્રિંગ $0.5\, cm$ જેટલી ખેંચાઇ છે. અને પરિપથનો કુલ અવરોધ $12\, \Omega $ છે. જ્યારે નીચેના તાર પર અચળ ચુંબકીય ક્ષેત્ર લગાવવામાં આવે ત્યારે સ્પ્રિંગ $0.3\, cm$જેટલી વધારે ખેંચાઇ છે. તો લગાવેલ ચુંબકીયક્ષેત્ર કેટલું હશે?View Solution
- 3જેમાં $I$ જેટલો વિદ્યુતપ્રવાહ વહે છે તેવા એક સુવાહક તારને $N$ આંટા ધરાવતા વર્તુળાકાર ગૂંચળામાં વાળવામાં આવે છે ત્યાર બાદ તેને $n$ આંટા ધરાવતાં વર્તુળાકાર ગૂંચળામાં વાળવામાં આવે છે. બંને ગૂંચળાના કેન્દ્ર આગળ ચુંબકીય ક્ષેત્ર ગણવામાં આવે છે. પ્રથમ કિસ્સામાં અને બીજા કિસ્સામાં મળતા ચુંબકીય ક્ષેત્રનો ગુણોતર $.............$ થશે.View Solution
- 4નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $I$ :બાયો-સાર્વટનો નિયમ પ્રવાહ ધરાવતા સુવાહકના ફક્ત અતિસુક્ષ્મ વિદ્યુતખંડ $(Idl)$ ને કારણે ઉત્પન્ન ચુંબકીય ક્ષેત્રની તીવ્રતાનું સૂત્ર આપે છે.
વિધાન $II$ :બાયો-સાર્વટનો નિયમ વીજભાર $q$ માટે કુલંબના પ્રતિવર્ગના નિયમ જેવો જ છે, કે તેમાં પ્રથમ એ અદિશ ઉદગમ $Idl$ ને કારણે ઉત્પન્ન ક્ષેત્ર સાથે સંકળાયેલ છે જ્યારે પછીનો એ સદિશ ઉદગમ $q$ ને કારણે ઉત્પન્ન ક્ષેત્ર સાથે સંકળાયેલ છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સૌથી યોગ્ય વિક્લ્પ પસંદ કરો.
- 5$0.1\, m $ ત્રિજયા અને $500 $ આંટા ધરાવતા ટોરોઇડમાં $0.5\, ampere $ પ્રવાહ પસાર કરતાં તેમાં ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 6બે સમાંતર રહેલા પ્રવાહધારિત તાર વચ્ચેનું અંતર $b$ છે.તો એક તાર દ્વારા બીજા તારના એકમ લંબાઇ દીઠ કેટલું બળ લાગશે?View Solution
- 7$R$ ત્રિજ્યા ધરાવતી પાતળી વર્તુળાકાર તકતીને $\sigma$ જેટલી સમાન પૃષ્ઠ ધનતા વડે વિદ્યુતભારિત કરવામાં આવે છે. $(\sigma>0)$ તક્તી તેના કેન્દ્રની સાપેક્ષે અચળ કોણીય ઝડપ $\omega$ થી ભ્રમણ કરે છે. તો તક્તીની ચુંબકીય ચાકમાત્રા કેટલી હશે?View Solution
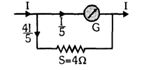
- 8જ્યારે $4\,\Omega$ ના શંટને ગેલ્વેનોમીટર સાથે જોડવામાં આવે તો વિચલન $1/5$ જેટલું ઘટે છે. જો વધારાનો $2\,\Omega$ નો શંટ જોડવામાં આવે તો વિચલન કેટલું હશે ?View Solution
- 9$25\,cm ^2$ નું ક્ષેત્રફળ ધરાવતા એક ચોરસગાળાનો અવરોધ $10\,\Omega$ છે. ગાળાને $40.0\,T$ ધરાવતા નિયમિત ચુંબકીય ક્ષેત્રમાં મૂકવામાં આવેલ છે. ગાળાનું સમતલ ચુંબકીયક્ષેત્રને લંબ છે. ગાળાને $1.0$ સેકન્ડના ગાળામાં ધીમે-ધીમે ચુંબકીયક્ષેત્રમાંથી બહાર કાઢવા માટે થતું કાર્ય $..........\times 10^{-3}$ હશે.View Solution
- 10ઇલેક્ટ્રોન ઘન $+x$ દિશામાં $6 \times 10^{6}\, ms ^{-1}$ ના વીગથી ગતિ કરે છે. વિધુતક્ષેત્ર $+ y$ દિશામાં $300 \,V / cm$ છે. ઇલેક્ટ્રોન $+ x-$ દિશામાં ગતિ કરે તે માટે ચુંબકીયક્ષેત્રનું મૂલ્ય અને દિશાView Solution
