$R$ ત્રિજ્યા ધરાવતી પાતળી તકતીની વિજભાર ઘનતા $\sigma $ છે. તકતીના કેન્દ્ર આગળ વિદ્યુતક્ષેત્ર $\frac{\sigma }{{2\,{ \in _0}}}$ છે.કેન્દ્ર આગળ રહેલ ક્ષેત્રની સાપેક્ષમાં કેન્દ્રથી $R$ અંતરે રહેલ અક્ષ પર વિદ્યુતક્ષેત્ર ....
JEE MAIN 2013, Diffcult
a
Electric field intensity at the centre of the disc.
Electric field intensity at the centre of the disc.
\(E=\frac{\sigma}{2 \epsilon_{0}} \quad(\text { given })\)
Electric field along the axis at any distance
\(x\) from the centre of the disc
\(E^{\prime}=\frac{\sigma}{2 \epsilon_{0}}\left(1-\frac{x}{\sqrt{x^{2}+R^{2}}}\right)\)
From question, \(x=R(\text { radius of disc })\)
\(\therefore \mathrm{E}^{\prime}=\) \( \frac{\sigma}{2 \epsilon_{0}}\left(1-\frac{\mathrm{R}}{\sqrt{\mathrm{R}^{2}+\mathrm{R}^{2}}}\right) \)
\(= \frac{\sigma}{2 \epsilon_{0}}\left(\frac{\sqrt{2} \mathrm{R}-\mathrm{R}}{\sqrt{2} \mathrm{R}}\right) \)
\(=\frac{4}{14} \mathrm{E}\)
\(\therefore\) \(\%\) reduction in the value of electric field
\(=\frac{\left(\mathrm{E}-\frac{4}{14} \mathrm{E}\right) \times 100}{\mathrm{E}}=\frac{1000}{14} \%=70.7 \%\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
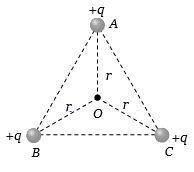
- 1સમબાજુ ત્રિકોણ $ABC$ ના દરેક શિરોબિંદુ પર $ + \,q$ વિજભાર મૂકેલા છે તો $O$ બિંદુ પાસે વિદ્યુતક્ષેત્રની તીવ્રતા કેટલી થાય?View Solution
- 2$q_1$ બિંદુવત વિદ્યુતભાર $q_2$ વિદ્યુતભાર પર $F$ બળ લાગુ પાડે છે. જો બીજો એક વિદ્યુતભાર $q_3$ ને $q_2$ વિદ્યુતભારની એકદમ નજીક મૂકવામાં આવે તો $q_1$ વિદ્યુતભાર દ્વારા $q_2$ વિદ્યુતભાર પર લાગતું બળ કેટલું હશે ?View Solution
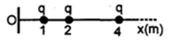
- 3View Solutionનીચે આપેલ આકૃતિમાં ઊગમબિંદુ આગળ અનંત સંખ્યાના વિદ્યુતભારને લીધે વિદ્યુતક્ષેત્રની ગણતરી કરો.
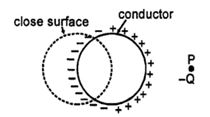
- 4આકૃતિમાં દર્શાવ્યા મુજબ બંધ પૃષ્ઠ ગોળીય વાહકમાંથી પસાર થાય છે. જો ઋણ વિદ્યુતભારને $P$ બિંદુ આગળ મૂકવામાં આવે તો બંધ પૃષ્ઠમાંથી બહાર આવતા વિદ્યુત ફલક્સનો સ્વભાવ કેવો હશે ?View Solution
- 5$0.1 \,\mu m$ ત્રિજ્યાનો એક વિદ્યુતભારતીત પાણીનું ટીપુ વિદ્યુતક્ષેત્રની સંતુલન અવસ્થા હેઠળ આવેલ છે. ટીપા પરનો વિદ્યુતભાર ઈલેકટ્રોનીક્સ વિદ્યુતભારને સમતુલ્ય છે. વિદ્યુતક્ષેત્રની તીવ્રતા ........$N/C$ છે.View Solution
- 6$8$ $\mu g$ દળ અને $39.2 \times {10^{ - 10}}$ વિદ્યુતભાર ધરાવતા ગોળાથી બનાવેલ સાદા લોલક પર સમક્ષિતિજ દિશામાં $20 \times {10^3}\ volt/meter$ વિદ્યુતક્ષેત્ર લગાવતાં,દોરી શિરોલંબ સાથે કેટલા .......$^o$ નો ખૂણો બનાવે?View Solution
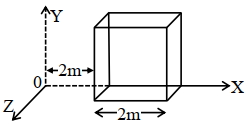
- 7અવકાશમાં $\vec{E}=(2 x \hat{i}) N C^{-1}$ જેટલું વિદ્યુતક્ષેત્ર પ્રવર્ત છે. નીચે દર્શાવેલ આકૃતિ મુજબ $2 \mathrm{~m}$ બાજુ ધરાવતો સમધન આ વિસ્તારમાં મૂકવામાં આવે છે : સમધનમાંથી પસાર થતું ફ્લકસ ........... $\mathrm{Nm}^2 / \mathrm{C}$ હશે.View Solution
- 8$R$ ત્રિજ્યા ધરાવતી પાતળી તકતીની વિજભાર ઘનતા $\sigma $ છે. તકતીના કેન્દ્ર આગળ વિદ્યુતક્ષેત્ર $\frac{\sigma }{{2\,{ \in _0}}}$ છે.કેન્દ્ર આગળ રહેલ ક્ષેત્રની સાપેક્ષમાં કેન્દ્રથી $R$ અંતરે રહેલ અક્ષ પર વિદ્યુતક્ષેત્ર ....View Solution
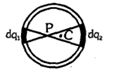
- 9સમાન વિદ્યુતભારતી ગોળીય કવચના $q_1$ અને $q_2$ ખંડને લીધે $P$ બિંદુ આગળ ચોખ્ખું વિદ્યુતક્ષેત્ર ...... છે. $( C $ એ કવચનું કેન્દ્ર આપેલ છે.$)$View Solution
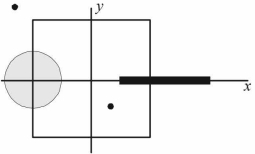
- 10$a/4$ ત્રિજ્યાની તકતી જે સમાન વિતરણ વિજભાર $6 c$ ધરાવે છે. તેને $x - y$ સમતલમા $(-a / 2,0,0)$ કેન્દ્ર સાથે તે માં મૂકવામાં આવે છે.$a$ લંબાઈનો સળિયો જે સમાન વિતરણ વીજભાર $8c$ ધરાવે છે તેને $X = a / 4$ થી $X =5 a / 4$ સુધી $X - axis$ પર મૂકેલ છે. જો બિંદુવત વીજભાર $-7 c$ અને $3 c$ ને $(a / 4,-a / 4,0)$ પર અને $(-3 a / 4,3 a / 4,0)$ પર મૂકેલ છે.બે સપાટી, $x=\pm a / 2, \quad Y =\pm a / 2, \quad Z =\pm a / 2$ દ્વારા બનતા ગોળાકાર સપાટીને ધ્યાનમાં લો. તેમાંથી પસાર થતું વિદ્યુત ફ્લક્સ $..........$View Solution