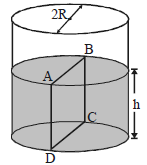
$R$ ત્રિજ્યાના બીકરમાં $h$ ઊંચાઈ સુધી પાણી ભરવામાં આવે છે.પાણી ની ઘનતા $\rho$,પૃષ્ઠતાણ $T$ અને વાતાવરણનું દબાણ $P_0$ છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે એક આડછેદ $ABCD$ લો.આ આડછેદના એક બાજુના પાણી દ્વારા બીજી બાજુના પાણી પર કેટલા મૂલ્યનું બળ લાગે?
Medium
Download our app for free and get started
\(Net\,force = Average\,pressure \times Area - T \times 2R\)
\(\left( {{P_0} + \rho g\frac{h}{2}} \right)\left( {2Rh} \right) - T2R\)
\( \Rightarrow \left| {2\,{P_0}Rh + R\rho g{h^2} - 2RT} \right|\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$4\,cm$ ત્રિજ્યાનો સાબુનો પરપોટો બીજા $6\,cm$ ત્રિજ્યાના પરપોટામાં તેને સંપર્ક કર્યા સીવાય ફસાયેલ છે.$P_2$ એ અંદરના પરપોટાની અંદરનું દબાણ અને $P_0$ એ બહારના પરપોટાની બહારનું દબાણ છે.બીજા એક પરપોટોની ત્રિજ્યા જેની અંદર બહારના દબાણનો તફાવત $P_2 - P_0$ હોય? ....... $cm$View Solution
- 2એક $R$ ત્રિજ્યા ધરાવતા પ્રવાહી બુંદને એકસમાન $27$ પ્રવાહી બુંદીમાં વિભાજિત કરવામાં આવે છે. જો પૃષ્ઠતાણ $T$ હોય, તો આ પ્રક્રિયામાં થતું કાર્ય_______થશે.View Solution
- 3View Solutionએક સાબુના પરપોટામાં અંદરનું દબાણ બીજા પરપોટાના અંદરના દબાણ કરતાં ત્રણ ગણું છે તો તેમના કદનો ગુણોત્તર કેટલો થાય?
- 4એક પોલા ગોળામાં નાનું છિદ્ર હોય છે, જ્યારે તેની પાણીની સપાટીની નીચે $40 \,cm$ ઊંડાઈએ લઈ જવામાં આવે છે, ત્યારે જ તેમાં પાણી દાખલ થાય છે. પાણીનું પૃષ્ઠતાણ $0.07 \,N / m$ છે. છિદ્રનો વ્યાસ ........... $mm$.View Solution
- 5નીચે બે વિધાનો આપેલા છે :View Solution
વિધાન $I$: જ્યારે કેશનળીને પ્રવાહીમાં ડૂબાડવામાં આવે છે ત્યારે પ્રવાહી કેશનળીમાં ઉપર ચઢતું નથી કે નીચે પણ ઉતરતું નથી. સંપર્કકોણ $0^{\circ}$ હોય શકે છે.
વિધાન $II$ : ધન અને પ્રવાહી વચ્ચેનો સંપર્કકોણ ધન દ્રવ્યના અને પ્રવાહી દ્રવ્યના ગુણધર્મ પર પણ આધારીત છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભરમાં, નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 6$r$ ત્રિજ્યાવાળા પારાના બે ટીપા ભેગા થઈને મોટું ટીપું બનાવે છે. જો પૃષ્ઠતાણ $T$ હોય, તો મોટા ટીપાની પૃષ્ઠઊર્જા કેટલી હશે?View Solution
- 7View Solutionપ્રવાહી સાથે સપાટીને ભીની કરવી મુખ્યત્વે શાના પર નિર્ભર છે?
- 8View Solutionકેશનળીમાં પ્રવાહીની મેનિકસ બર્હિગોળ હોય,ત્યારે સંપર્કકોણ કેટલો હોય?
- 9$30 \,dynes\, per\, cm $ પૃષ્ઠતાણ ધરાવતા $\frac{1}{{\sqrt \pi }}\,cm$ ત્રિજયાના પરપોટાની ત્રિજયા $\frac{2}{{\sqrt \pi }}\,cm$ કરવા માટે ....... $ergs$ કાર્ય કરવું પડે.View Solution
- 10$0.015\;cm$ ત્રિજ્યા ધરાવતી કાંચની લાંબી કેશનળીને પ્રવાહીમાં ડૂબાડતા તેમાં પ્રવાહી $15\, cm$ જેટલું ઉપર ચડે છે જો પ્રવાહીની સપાટી અને પાત્ર વચ્ચેનો સંપર્કકોણ $0^{\circ}$ હોય તો પ્રવાહીનું પૃષ્ઠતાણ $milli\,Newton \;m ^{-1}$ એકમમાં કેટલું હશે?View Solution
[પ્રવાહીની ઘનતા $\left.\rho_{\text {(liquid) }}=900\; kg\,m ^{-3}, g =10\, ms ^{-2}\right]$ (નજીકના પૂર્ણાંકમાં જવાબ આપો)