$R$ ત્રિજયાના વર્તુળમાં ગતિ કરતા કણની ગતિઊર્જા $k = a{s^2}$ છે.જયાં $s$ એ સ્થાનાંતર છે.તો કણ પર કેટલું બળ લાગતું હશે?
Diffcult
b
(b) According to given problem \(\frac{1}{2}m{v^2} = a{s^2}\) \( \Rightarrow v = s\sqrt {\frac{{2a}}{m}} \)
(b) According to given problem \(\frac{1}{2}m{v^2} = a{s^2}\) \( \Rightarrow v = s\sqrt {\frac{{2a}}{m}} \)
So \({a_R} = \frac{{{v^2}}}{R} = \frac{{2a{s^2}}}{{mR}}\)…\((i)\)
Further more as \({a_t} = \frac{{dv}}{{dt}} = \frac{{dv}}{{ds}} \cdot \frac{{ds}}{{dt}} = v\frac{{dv}}{{ds}}\)…\((ii)\) (By chain rule)
Which in light of equation \((i)\) i.e. \(v = s\sqrt {\frac{{2a}}{m}} \) yields
\({a_t} = \left[ {s\sqrt {\frac{{2a}}{m}} } \right]\,\left[ {\sqrt {\frac{{2a}}{m}} } \right] = \frac{{2as}}{m}\)…\((iii)\)
So that \(a = \sqrt {a_R^2 + a_t^2} = \sqrt {{{\left[ {\frac{{2a{s^2}}}{{mR}}} \right]}^2} + {{\left[ {\frac{{2as}}{m}} \right]}^2}} \)
Hence \(a = \frac{{2as}}{m}\sqrt {1 + {{[s/R]}^2}} \)
\(F = ma = 2as\sqrt {1 + {{[s/R]}^2}} \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $M$ દળનો પદાર્થ વજનરહિત દોરી વડે લટકાવેલ છે. દોરીને શિરોલંબ સાથે $45^{\circ}$ ના ખૂણે ગોઠવવા માટે પદાર્થ પર કેટલું સમક્ષિતિજ બળ લગાડવું પડે?View Solution
- 2$k$ બળ અચળાંક ધરાવતી સ્પ્રિંગની લંબાઇ $ x = 0 $ થી $ x = {x_1} $ વધારતાં કેટલું કાર્ય થશે?View Solution
- 3કોલમ $-I$ અને કોલમ $-II$ સાથે જોડો.View Solution
કોલમ $-I$ કોલમ $-II$ $(1)$ થયેલું કાર્ય શૂન્ય $(a)$ ગુરુત્વાકર્ષણ બળ વડે $(2)$ થયેલું કાર્ય ધન $(b)$ ગુરુત્વાકર્ષણ બળની વિરુદ્ધ $(3)$ થયેલું કાર્ય ઋણ $(c)$ કેન્દ્રગામી બળ વડે - 4એક પદાર્થને જમીનથી $h$ ઊંચાઈ એ થી મુક્ત કરવામાં આવે છે. જેટલી વાર તે જમીન પર અથડાય ત્યારે તે તેની ગતિઉર્જા ના $50\%$ જેટલી ગતિઉર્જા ગુમાવે છે. તો $t \to \infty $ દરમ્યાન તેણે કાપેલ અંતર કેટલું હશે?View Solution
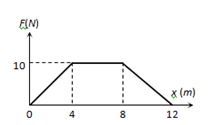
- 5$0.1 kg $ દળ ધરાવતા કણ પર આકૃતિમાં દર્શાવ્યા પ્રમાણે અંતરની સાપેક્ષે બળ લગાડવામાં આવે છે. જો તે $x = 0$ એ સ્થિર સ્થિતીથી શરૂ કરે તો $x = 12$ એ તેનો વેગ ....... $m/s$View Solution
- 6બળ $\vec{F}=(2+3 x) \hat{i}$ એ એક કણ ઉપર $x$ દિશામાં પ્રવર્તે છે, જ્યાં $F$ એ ન્યૂટનમાં અને $x$ મીટરમાં છે. $x=0$ થી $x=4\,m$ ના સ્થાનાંતર દરમ્યાન આ બળ દ્વારા થતું કાર્ય .....$J$ હશે.View Solution
- 7એક બોલ $ 'h' $ ઉંચાઈ પરથી મુક્ત રીતે પતન કરે છે. આ બોલ સતત પટકાઈને પાછો ફરે છે. તો $ 'n' $ વાર પાછો ફર્યા પછી બોલ વડે પ્રાપ્ત થતી ઉંચાઈ અને $n$ વાર પાછો ફરવા માટે બોલને લાગતો સમય શોધો.View Solution
- 8$30\, kg$ દળવાળો સ્થિર બોમ્બ વિસ્ફોટ પામીને $18 \,kg$ અને $12\, kg$ દળના બે ટુકડા થાય છે. $18 \,kg$ દળવાળા ટુકડાનો વેગ $6\; ms^{-1}$ છે. બીજા ટુકડાની ગતિઊર્જા ($J$ માં) કેટલી થાય?View Solution
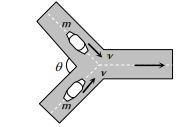
- 9View Solutionસમાન દળ અને સમાન વેગથી જતી બે કાર વચ્ચે સંપૂર્ણ અસ્થિતિસ્થાપક અથડામણ થતાં બંને કારનો વેગ
- 10$100 m $ લંબાઇ અને $1 m$ ઉંચાઇ ધરાવતા ઢાળ પર $30,000 kg$ નો ટ્રક $30 km/hr$ ની ઝડપથી ગતિ કરે,તો ટ્રકનો પાવર કેટલા .......... $kW$ થશે? $( g = 10m{s^{ - 1}}) $View Solution
