રાસાયણિક સંતુલન માટે, $CaC{{O}_{3}}_{(s)})$ $\rightleftharpoons$ $CaO_{(s)}+C{{O}_{2}}_{(g)},\ \Delta H_{r}^{{}^\circ }$ એ નીચેના પ્લોટમાંથી કયા પ્લોટમાંથી નક્કી કરી શકાય છે.
- A
- B
- C
- D
AIIMS 2005, Diffcult
Download our app for free and get started
a
For the reaction,
For the reaction,
\(CaCO_{3(g)} \rightleftharpoons CaO_{(s)} + CO_{2(g)}\)
\(K_p = P_{CO_2}\) and \(K_C = [CO_2]\)
\((\because [CaCO_3] = 1\) and \([CaO] = 1\) for solids\()\)
According to Arrhenius equation we have
\(K = A{e^{ - \Delta H{^\circ _r}/RT}}\)
Taking logarithm, we have
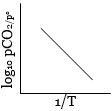
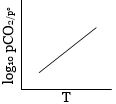
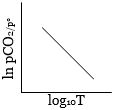
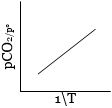
\(\log {K_p} = \log\, A - \frac{{\Delta H_r^o}}{{RT(2.303)}}\)
This is an equation of straight line. When \(log \,K_p\) is plotted against \(1 / T\). we get a straight line.
The intercept of this line = \( log \,A\), slope \(= -\Delta H^°_r / 2.303 \,R\)
Knowing the value of slope from the plot and universal gas constant \(R\), \(∆H^°_r\) can be calculated.
(Equation of straight line : \(Y = mx + C\). Here,
\(\log {K_p} = - \frac{{\Delta H_r^o}}{{2.303R}}\left( {\frac{1}{T}} \right) + \log A\)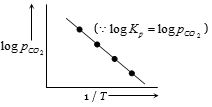
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$300\,\,K\,\,40\,\,\% HI$ પર વિધટન પામી $H _{2}$ અને $I _{2}$ બનાવે છે. એક વાતાવરણના દબાણે આ વિધટન પ્રક્રિયા માટે $\Delta G ^{\ominus}$ નું મૂલ્ય $\dots\dots\dots\,\,J\,mol ^{-1}$ શોધો. (નજીકના પૂર્ણાંકમાં)View Solution
(ઉપયોગ $R =8.31\, J\, K ^{-1}\, mol ^{-1} ; \log 2=0.3010$. In $10=$ $2.3, \log 3=0.477$ )
- 2પ્રક્રિયા $N_{2(g)} + O_{2(g)} $ $\rightleftharpoons$ $ 2NO_{(g)}$ અને $\frac{1}{2}{N_2} + \frac{1}{2}{O_2}$ $\rightleftharpoons$ $NO$ ના સંતુલન અચળાંક અનુક્રમે $K_1$ અને $K_2$ હોય તો તેમનો સંબંધ.....View Solution
- 3$H_2O_{(l)}$ $\rightleftharpoons$ $ H_2O_{(g)}$ સંતુલન પ્રક્રિયા માટે જો દબાણ વધે તો શું થાય છે ?View Solution
- 4View Solutionનીચેના પૈકી કઇ પ્રક્રિયામાં, પાત્રના કદનો વધારો નીપજોના સર્જનની તરફેણ કરશે ?
- 5પ્રક્રિયા ${A_{(g)}}\, + \,2{B_{(g)}}\, \rightleftharpoons \,\,2{C_{(g)}}$ માટે $2\,L$ કદના પાત્રમાં $A$ ના $1$ મોલ અને $B$ ના $1.5$ મોલ લેવામાં આવે છે. જો સંતુલને $C$ ની સાંદ્રતા $0.35\,M$ હોય, તો પ્રક્રિયાનો સંતુલન અચળાંક $K_c$ .......$M^{-1}$ થશે.View Solution
- 6$5.1\, g\, NH_4SH$ ને $327^oC$ પર એક $3.0\,L$ (નિર્વાતિત)ખાલી કરેલા ફ્લાસ્કમાં નાખવામાં આવે છે. $30\%$ જેટલા ઘન $NH_4SH$ નું $NH_3$ અને $HS$ વાયુ સ્વરૂપે વિઘટન થાય છે. તો $327^oC$ પર પ્રક્રિયાનો $K_p$ કેટલો થશે?View Solution
($R = 0.082\, L\, atm\, mol^{-1}\, K^{-1}$, મોલર દળ $S = 32\, g\, mol^{-1}$, મોલર દળ $N = 14\, g\, mol^{-1}$)
- 7સંતુલન પ્રક્રિયા માટે $\Delta G°= 0$, સંતુલન અચળાંક $k$ = ........View Solution
- 8એક પ્રક્રિયા માટે $\Delta G° = -115$ કિલોજૂલ છે, તો $298 \,K$ તાપમાને $log\, K_p$ = …..View Solution
- 9પ્રક્રિયા ${N_{2(g)}} + {O_{2(g)}}$ $\rightleftharpoons$ $2N{O_{(g)}}$ માટે $T$ તાપમાને સંતુલન અચળાંક $4 \times {10^{ - 4}}$ છે. તો પ્રક્રિયા $N{O_{(g)}}$ $\rightleftharpoons$ $\frac{1}{2}{N_{2(g)}} + \frac{1}{2}{O_{2(g)}}$ માટે આ જ તાપમાને સંતુલન અચળાંક ............. થશે.View Solution
- 10પ્રક્રિયા $N_2$$_{(g)}$ $+$ $O_2$$_{(g)}$ $\rightleftharpoons$ $2NO$$_{(g)}$ માટે સંતુલન અચળાંક $K_1$ છે તથા પ્રક્રિયા $2NO$$_{(g)}$ $+$ $O_2$$_{(g)}$ $\rightleftharpoons$ $2N$$O_2$$_{(g)}$ માટે સંતુલન અચળાંક $K_2$ છે. તો પ્રક્રિયા $N$$O_2$$_{(g)}$ $\rightleftharpoons$$\frac{1}{2}{N_{2(g)}}\, + \,\,{O_{2(g)}}$માટે સંતુલન અચળાંક $K$ ની કિમત......થશે.View Solution