રેડિયો-ઍક્ટિવ પદાર્થનો અર્ધઆયુ $20$ મિનિટ છે. $20\%$ અને $80\%$ વિભંજન વચ્ચેનો સમયગાળો ........ મિનિટ હશે.
Diffcult
Download our app for free and get started
b
અહીં, \(t_{1/2} = 20\) મિનિટ. આપણે જાણીએ છીએ કે,
અહીં, \(t_{1/2} = 20\) મિનિટ. આપણે જાણીએ છીએ કે,
\(\frac{N}{{{N_0}}} = {\left( {\frac{1}{2}} \right)^{t/{\tau _{1/2}}}}\)
\(20\% \) વિભજન માટે
\(\frac{{\text{N}}}{{{{\text{N}}_{\text{0}}}}} = \frac{{80}}{{100}} = {\left( {\frac{1}{2}} \right)^{{t_1}/20}}\,\,\,....(1)\)
\(80\% \,\) વિભજન માટે
\(\frac{{\text{N}}}{{{{\text{N}}_{\text{0}}}}} = \frac{{20}}{{100}} = {\left( {\frac{1}{2}} \right)^{{t_2}/20}}\,......(2)\)
સમીકરણ \((2)\) ને સમીકરણ વડે ભાંગતા (\(\frac{1}{4} = {\left( {\frac{1}{2}} \right)^{\frac{{({t_2} - {t_1})}}{{20}}}}\)
સાદું રૂપ આપતાં, \(t_2 - t_1 = 40\) મિનિટ
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક તાજો તૈયાર કરેલ $2\, h$ નો અર્ધઆયુ ધરાવતાં રેડિયોએક્ટિવ સ્ત્રોત એ સ્વીકાર્ય સુરક્ષિત સ્તર કરતાં $64$ ગણી રેડિએશનની તીવ્રતાનો સ્રાવ કરે છે. તો આ સ્ત્રોત સાથે શક્ય એટલું કામ કરવા માટેનો ઓછામાં ઓછો સમય ....... $h$ છે.View Solution
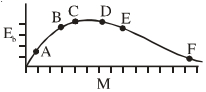
- 2ન્યુકિલયોનદીઠ બંધનઊર્જા $E_{bn}$ વિરુદ્ઘ જુદા જુદા ન્યુકિલયસ $A, B,C,D,E$ અને $F$ માટેના ન્યુકિલયર દળ $(M)$ માટેનો આલેખ નીચે મુજબ છે.ધારો કે, ચાર પ્રક્રિયા નીચે મુજબ છે :View Solution
$(i)\;A+B\;\to\; C \;+\;\varepsilon $
$(ii)\;C\;\to \;A\;+\;B\;+\;\varepsilon $
$(iii)\;D\;+\;E\;\to \; F\;+$$\;\varepsilon $
$(iv)\;F\;\to \; D\;+\;E\;+\;\varepsilon $
જયાં,$\;\varepsilon $ એ મુકત થતી ઊર્જા છે.કઇ પ્રક્રિયામાં $\varepsilon $ ધન હશે?
- 3કોઈ ચોક્કસ રેડીયોએક્ટિવ નમૂનાનો કોઈ ક્ષણે વિભંજન દર $4250$ વિખંડન પ્રતિ મીનીટ છે. $10$ મીનીટ બાદ, દર $2250$ વિખંડન પ્રતિ મીનીટ થાય છે. ક્ષય નિયતાંક $.........\min^{-1}$ થશે.View Solution
$\left(\log _{10} 1.88=0.274\right.)$ લો.
- 4એવોગ્રેડો નંબર $6 \times 10^{23}$ છે. $14 \,g\,\, _6{C^{14}}$ માં પ્રોટોન,ન્યુટ્રોન અને ઇલેકટ્રોનની સંખ્યા કેટલી હશે?View Solution
- 5નીચે આપેલા રેડીયો એકિવિવીટીને લગતાં વિધાનોમાંથી સાચું અવલોકન શોધો :View Solution
$(A)$ રેડીયોએક્વિવીટી એ યાદચ્છિક (અસ્તવ્યસ્ત) અને તત્ક્ષણિક પ્રક્રિયા છે કે જે ભૌતિક અને રસાયણિક સ્થિતિઓ ઉપર આધાર રાખે છે.
$(B)$ રેડીયોએકિટવ નમૂનામાં ક્ષય ન પામેલા ન્યુક્લિયસો સમય સાથે ચરઘાતાંકીય રીતે ક્ષય પામે છે.
$(C)$ $\log _{ e }$ (ક્ષય ન પામેલા ન્યુક્લિયાસોની સંખ્યા) વિરુધ્ધ સમય આલેખનો ઢાળ સરેરાશ સમય $(\tau)$ નો વ્યસ્ત આપે છે.
$(D)$ ક્ષય અચળiક $(\lambda)$ અને અર્ધ-જીવન કાળ $\left( T _{1 / 2}\right)$ નો ગુણાકાર અચળ નથી.
નીચે આપેલા વિકલ્પોમાંથી સાંચુ વિકલ્પ પસંદ કરો :
- 6ડયુટેરોન અને $\alpha -$ કણ માટે ન્યુકિલયોનદીઠ બંધન-ઊર્જા અનુક્રમે $x_1$ અને $x_2$ છે. નીચે આપેલ પ્રક્રિયામાં મુક્ત થતી ઊર્જા $Q$ કેટલી હશે?View Solution
$_1{H^2}{ + _1}{H^2}{ \to _2}H{e^4} + Q$
- 7ન્યુક્લિયસ, ન્યુટ્રોન અને પ્રોટોનનું દળ અનુક્રમે $M, M_n$ અને $M_p$ છે. ત્યારે ......View Solution
- 8બે જુદા જુદા એક્ટિવ ન્યુક્લિયસના નમૂનાનો ગુણોત્તર $2 : 3$ છે. તેમનું અર્ધ આયુષ્ય અનુક્રમે $1$ કલાક અને $2$ કલાક છે. $6$ કલાક બાદ એક્ટિવ ન્યુક્લિયસનો ગુણોત્તર .......થશે.View Solution
- 9View Solutionન્યક્લિયર રીએક્ટરની પ્રક્રિયાને ક્રીટીકલ કહે છે, જ્યારે મલ્ટીપ્લીકેશન ફેક્ટરની કિંમત .......હોય છે.
- 10View Solutionન્યુક્લિયર રીએક્ટરમાં બોરોન સળિયાનો ઉપયોગ ......તરીકે થાય છે.