$\rho(r)=\left\{\begin{array}{ll}\rho_{0}\left(\frac{3}{4}-\frac{r}{R}\right) & \text { for } r \leq R \\ \text { Zero } & \text { for } r>R\end{array}\right.$
અનુસાર બદલાતી ગોલીય સંમિત વિદ્યુતભાર વહેંચણી વિચારો,જ્યાં $r ( r < R )$ એ કેન્દ્રથી અંતર છે (આકૃતિ જુઓ) $P$ બિંદુ આગળ વિદ્યુતક્ષેત્ર $......$ હશે.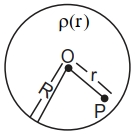
JEE MAIN 2022, Diffcult
c
\(\oint \overrightarrow{ E } \cdot d \overrightarrow{ s }=\frac{ Q _{\text {in }}}{\varepsilon_{ o }}\)
\(\oint \overrightarrow{ E } \cdot d \overrightarrow{ s }=\frac{ Q _{\text {in }}}{\varepsilon_{ o }}\)
\(E .4 \pi r ^{2}=\frac{\int_{0}^{ r } \rho_{ o }\left(\frac{3}{4}-\frac{ r }{ R }\right) 4 \pi r ^{2} dr }{\varepsilon_{0}}\)
\(E 4 \pi r ^{2}=\frac{\rho_{ o } 4 \pi}{\varepsilon_{ o }}\left(\frac{3}{4} \frac{ r ^{3}}{3}-\frac{ r ^{4}}{4 R }\right)\)
\(Er { }^{2}=\frac{\rho_{ o } r ^{3}}{4 \varepsilon_{ o }}\left\{1-\frac{ r }{ R }\right\}\)
\(E =\frac{\rho_{0} r }{4 \varepsilon_{ o }}\left\{1-\frac{ r }{ R }\right\}\)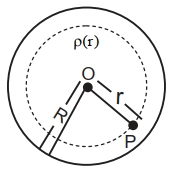
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ઉગમ બિંદુથી $x-$ અક્ષ પર ત્રણ વિદ્યુતભારો $+Q, q$ અને $+Q $ અનુક્રમે $0,\frac d2$ અને $d$ આગળ મુકેલ છે. જો $x=0$ આગળ મુકેલ $+Q$ દ્વારા અનુભવાતું કુલ બળ શૂન્ય હોય તો $q$ નું મૂલ્ય કેટલું હશે.View Solution
- 2$h$ ઊંચાઈ અને $R$ બેજની ત્રિજ્યા ધરાવતા શંકુને $\vec E$ વિદ્યુતક્ષેત્રમાં એવી રીતે મૂકવામાં આવે છે કે જેથી વિદ્યુતક્ષેત્ર બેજને સમાંતર રહે.તો શંકુમાં દાખલ થતું વિદ્યુત ફ્લક્સ કેટલું હશે?View Solution
- 3View Solutionબળના વિદ્યુત રેખાને લાગતું સાચું વિધાન પસંદ કરો.
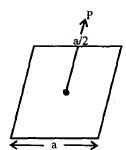
- 4$a$ બાજુવાળા ચોરસના કેન્દ્રથી $a/2$ અંતર ઉપરની દિશામાં $Q$ વિજભાર મૂકેલો છે. ચોરસની સપાટીમાંથી પસાર થતું વિદ્યુતફ્લક્સ કેટલું મળે?View Solution
- 5દરેક $m$ જેટલું દળ અને $q$ જેટલો વિદ્યુતભાર ધરાવતા બે એકસમાન ટેનિસ બોલને $l$ લંબાઈની દોરી વડે જડિત બિંદુથી લટકવવામાં આવેલ છે. જ્યારે શિરોલંબ સાથે દરેક દોરી નાનો કોણ $\theta$ રચતી હોય તો ત્યારે સંતુલન સ્થિતિમાં અંતર .......... હશે?View Solution
- 6$a$ બાજુવાળા સમબાજુ ત્રિકોણના શિરોબંદુ પર $+Q$ વિદ્યુતભાર મૂકેલા છે.તો એક વિદ્યુતભાર પર લાગતું બળ કેટલું થાય? $\left( {k = \frac{1}{{4\pi {\varepsilon _0}}}} \right)$View Solution
- 7ધારો કે સમાન વિદ્યુતભારિત દિવાલ $2 \times 10^4 \mathrm{~N} / \mathrm{C}$ મૂલ્યનું એક લંબ સમાન વિદ્યુતક્ષેત્ર આપે છે. એક $2 \mathrm{~g}$ દળના વિદ્યુતભારિત કણને $20 \mathrm{~cm}$ લંબાઈના સિલ્કના દોરા વડે લટકાવવામાં આવે છે અને તે દિવાલ થી $10 \mathrm{~cm}$ દૂર રહે છે. કણ પરનો વિદ્યુતભાર $\frac{1}{\sqrt{x}}$ $\mu \mathrm{C}$ હોયતો $x$=__________થશે. $[g=10 m/s$View Solution
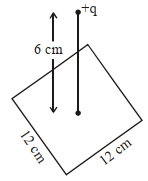
- 8આકૃત્તિમાં દર્શાવ્યા પ્રમાણે $12\, cm$ ની બાજુ ધરાવતાં એક ચોરસની શિરોલંબ ઉપર $6\, cm$ અંતરે $+\,12 \,\mu C$ નાં એક બિંદુવર વીજભાર રહેલ છે. ચોરસમાંથી પસાર થતાં વિદ્યુતફ્લકસનું મૂલ્ય ....... $\times 10^{3} \,Nm ^{2} / C$ થશે.View Solution
- 9$\mathrm{m}$ દળ અને $\mathrm{q}$ વિજભારને એકસમાન વિદ્યુતક્ષેત્રમાં મુક્ત કરવામાં આવે છે.જો કણ પર બીજા કોઈ પણ પ્રકારનું બળ લાગતું ના હોય તો કણ માટે વેગ $v$ વિરુદ્ધ અંતર $x$ નો આલેખ કેવો મળે?View Solution
- 10પોલા વાહક ગોળાની સપાટી પર $10\,\mu C$ વિધુતભાર આપવામાં આવે છે. જો ત્રિજ્યા $2\, m$ હોય, તો કેન્દ્ર પર વિદ્યુતક્ષેત્ર કેટલા........$\mu \,C{m^{ - 2}}$ થાય?View Solution
