\(\mathop A\limits^ \to \) અને \(\mathop B\limits^ \to \) વચ્ચેનો ખૂણો \( =110^0 - 20^0 = 90^0 \)
\(R\,\, = \,\,\sqrt {{A^2}\,\, + \;\,{B^2}\,\, + \;\,2AB\,\cos \,\,90^\circ } \,\, = \,\,\sqrt {{5^2}\,\, + \;\,{{12}^2}} \,\, = \,\,13m\)
સદીશ \(\mathop A\limits^ \to \) માથી \(\mathop R\limits^ \to \) નો ખૂણો \(\alpha \) છે તેમ લો.
\(\tan \,\,\alpha \,\, = \,\,\frac{{B\,\,\sin \,\,\theta }}{{A\,\, + \;\,B\,\,\cos \,\,\theta }}\,\, = \,\,\frac{{12\,\,\sin \,\,90^\circ }}{{5\,\, + \;\,12\,\,\cos \,\,90^\circ }}\,\, = \,\,\frac{{12\,\, \times \,\,1}}{{5\,\, + \;\,12\,\, \times \,\,0}}\,\, = \,\,\frac{{12}}{5}\)
અથવા \(\alpha \,\, = \,\,{\text{ta}}{{\text{n}}^{{\text{ - 1}}}}\,\,\left( {\frac{{12}}{5}} \right)\,\) સદીશ \(\mathop A\limits^ \to \) અથવા \(\left( {\alpha \,\, + \;\,20^\circ } \right)\,X\,\) અક્ષ સાથે 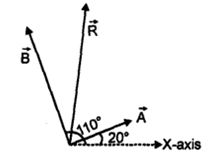
Download our appand get started for free
Similar Questions
- 1યામ પધ્ધતિમાં એક કણના યામ $(3, 2, 5)$ હોય તો તેનો સ્થાન સદીશ કેટલો થાય?View Solution
- 2$A = \hat i + \hat j$ સદિશનો $X$ અક્ષ સાથે બનતો ખૂણો ......$^o$ હશે.View Solution
- 3$5 \,N$ બળ શિરોલંબ સાથે $60^°$ ના ખૂણે લાગે છે,તો બળનો શિરોલંબ ઘટક......... $N$ મેળવો.View Solution
- 4$10\, N$ અને $6\, N$ બે બળોનો સદિશ સરવાળો ......... $N$ થઈ શકે નહીંView Solution
- 5એક સદિશ બિંદુ$\mathop {\rm{A}}\limits^ \to \,$શિરોલંબ ઊર્ધ્વ અને $\mathop B\limits^ \to $બિંદુ ઉત્તરમાં છે $\mathop A\limits^ \to \,\, \times \mathop B\limits^ \to $ નો સદિશ ગુણાકાર શું હશે ?View Solution
- 6જો સદિશ $ \overrightarrow A = 2\hat i + 4\hat j - 5\hat k $ ,હોય તો સદીશનો દિશાકીય cosine કેટલો થાય?View Solution
- 7જો $\overrightarrow{ F }=2 \hat{ i }+\hat{ j }-\hat{ k }$ અને $\overrightarrow{ r }=3 \hat{ i }+2 \hat{ j }-2 \hat{ k }$ હોય, તો $\overrightarrow{ F }$ અને $\overrightarrow{ r }$ ના અદિશ અને સદીશ ગુણકારનું મૂલ્ય અનુક્રમે કેટલું હશે?View Solution
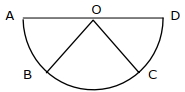
- 8વિધાન $A$ : જો $A, B, C, D$ એ અર્ધ વર્તુળ કેન્દ્ર $O$ પર ચાર બિંદુઓ એવા છે કે જેથી $|\overrightarrow{{AB}}|=|\overrightarrow{{BC}}|=|\overrightarrow{{CD}}|$ હોય, તો $\overrightarrow{{AB}}+\overrightarrow{{AC}}+\overrightarrow{{AD}}=4 \overrightarrow{{AO}}+\overrightarrow{{OB}}+\overrightarrow{{OC}}$View Solution
કારણ $R$ : સદીશ સરવાળાનો બહુકોણનો નિયમ $\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C D}+\overrightarrow{A D}=2 \overrightarrow{A O}$ આપે છે.
ઉપરોક્ત વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પો પૈકી સૌથી વધારે યોગ્ય જવાબ પસંદ કરો.
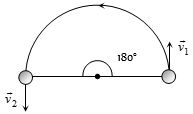
- 9આકૃતિમાં દર્શાવેલ કણ $5 \,ms^{-1}$ ની અચળ ઝડપથી ભ્રમણ કરે છે. તો અડધા પરિભ્રમણ દરમિયાન વેગમાં કેટલા ........$ms^{-1}$ નો ફેરફાર થાય?View Solution
- 10View Solutionસદીશમાં ફેરફાર શેના કારણો થાય છે ?
