શ્રેણીમા જોડેલા બે અવરોધોનો સમતુલ્ય અવરોધ $s$ છે.જયારે તેમને સમાંતર જોડવામાં આવે,તો સમતુલ્ય અવરોધ $p$ મળે છે.જો $s=np$ હોય,તો $n$ નું લઘુત્તમ મૂલ્ય કેટલું હોવું જોઈએ?
AIEEE 2004,JEE MAIN 2021, Diffcult
a
(a) If two resistances are \({R_1}\) and \({R_2}\) then
\(S = {R_1} + {R_2}\) and \(P = \frac{{{R_1}{R_2}}}{{({R_1} + {R_2})}}\)
From given condition \(S = nP\) i.e. \(({R_1} + {R_2}) = n\,\left( {\frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}} \right)\)
\(==>\) \({({R_1} + {R_2})^2} = n\,\,{R_1}{R_2}\) \(==>\) \({({R_1} - {R_2})^2} + 4{R_1}{R_2} = n{R_1}{R_2}\)
So \(n = 4 + \frac{{{{({R_1} - {R_2})}^2}}}{{{R_1}{R_2}}}.\) Hence minimum value of \(n\) is \(4\).
(a) If two resistances are \({R_1}\) and \({R_2}\) then
\(S = {R_1} + {R_2}\) and \(P = \frac{{{R_1}{R_2}}}{{({R_1} + {R_2})}}\)
From given condition \(S = nP\) i.e. \(({R_1} + {R_2}) = n\,\left( {\frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}} \right)\)
\(==>\) \({({R_1} + {R_2})^2} = n\,\,{R_1}{R_2}\) \(==>\) \({({R_1} - {R_2})^2} + 4{R_1}{R_2} = n{R_1}{R_2}\)
So \(n = 4 + \frac{{{{({R_1} - {R_2})}^2}}}{{{R_1}{R_2}}}.\) Hence minimum value of \(n\) is \(4\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
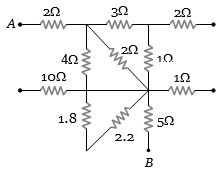
- 1આપેલ પરિપથમાં $A$ અને $B$ વચ્ચેનો સમતુલ્ય અવરોધ કેટલા .................. $\Omega$ થાય?View Solution
- 2ગાડીની લેડ-એસીડ કોષનો $e.m.f.$ $12\,V$ છે. કોષનો આંતરીક અવરોધ $0.5\,\Omega$ છે. તો કોષમાંથી મળતો મહત્તમ પ્રવાહ............. $A$ હશે.View Solution
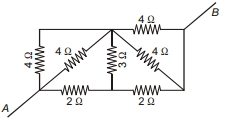
- 3આકૃતિમાં દશાવેલ પરિપથમાં $A B$ વચ્ચેનો અસરકારક $.......... \Omega$ અવરોધ છે.View Solution
- 4$20 \;{V}\; emf$ અને $10 \Omega$ આંતરિક અવરોધ ધરાવતી બેટરી સાથે પ્રથમ $10 \;\Omega$ અવરોધ ધરાવતા ${n}$ અવરોધોને શ્રેણીમાં જોડેલા છે. તેમાંથી પસાર થતો પ્રવાહ $I$ છે. હવે આ $n$ અવરોધોને સમાંતરમાં જોડીને સમાન બેટરી સાથે જોડાવામાં આવે તો પ્રવાહ $20$ ગણો થાય, તો $n$ નું મૂલ્ય કેટલું હશે?View Solution
- 5પોટેન્શિયોમીટર દ્વારા બે કોષનું તટસ્થ બિંદુ $20\, cm$ અને $30\,cm$ અંતરે મળે છે.તો બંને કોષનાં $emf$ નો ગુણોત્તર કેટલો થાય?View Solution
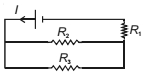
- 6દર્શાવેલ પરિપથના સંદર્ભમાં લઈ.જો $R_1$ માં વ્યય થતો પાવર $P$ હોય. તો, પરિપથમાં થતો કુલ પાવર .......... $P$ હોઈ શકે આપેલ છે કે $R_2=4 R_1$ અને $R_3=12 R_1$ છે.View Solution
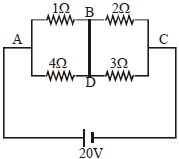
- 7આપેલ પરિપથમાં $B$ અને $D$ જોડતા તારમાં કેટલા .............. $A$ પ્રવાહનું વાહન થશે?View Solution
- 8બેટરી (કોષ) નો આંતરિક અવરોધ માપવા માટે પોટેન્શીયોમીટરનો ઉપયોગ કરવામાં આવે છે. $R=10 \Omega$ માટે તટસ્થ (સંતોલન) બિંદૂ$l=500 \mathrm{~cm}$ અંતરે અને $R=1 \Omega$ માટે તટસ્થ બિંદૂ $l=400 \mathrm{~cm}$ આગળ મળે છે. બેટરીનાં આંતરિક અવરોધનું સંનિક્ટ મૂલ્ય. . . . . . . થશે.View Solution
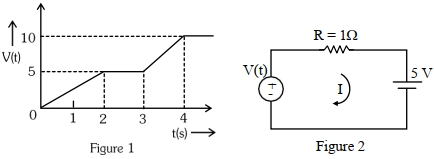
- 9આપેલ પરિપથ માટે ${t}=3.2\, {s}$ સમયે પ્રવાહ ........ ${A}$ હશે.View Solution
[Fig. $(1)$ માં વોલ્ટેજનું વિતરણ અને Fig. $(2)$ માં પરિપથ દર્શાવેલ છે]
- 10ત્રણ સમાન બેટરી $L$ લંબાઇના તાર સાથે શ્રેણીમાં જોડતા,તેના તાપમાનમાં $t$ સમયમાં જેટલો $\Delta T$ વઘારો થાય છે.$N$ બેટરીને સમાન દ્રવ્યના બનેલા $2L$ લંબાઇના તાર સાથે જોડતા,તેના તાપમાનમાં $t$ સમયમાં $\Delta T$ જેટલો વઘારો થાય છે તો $N=$ _____View Solution
