$\sigma$ પૃષ્ઠ ઘનતા ધરાવતી એકસમાન રીતે વિદ્યુતભારિત કરેલ $R$ ત્રિજ્યાની તકતીને ${xy}$ સમતલમાં ટકતીનું કેન્દ્ર ઉગમબિંદુ પર રહે તેમ મૂકેલી છે. તો $z-$ અક્ષ પર ઉગમબિંદુથી $Z$ અંતરે વિદ્યુતક્ષેત્રની તીવ્રતા કેટલી હશે?
JEE MAIN 2021, Diffcult
a
Consider a small ring of radius \({r}\) and thickness dr on disc.
Consider a small ring of radius \({r}\) and thickness dr on disc.
\([Image]\)
area of elemental ring on disc
\({d} {A}=2 \pi {rdr}\)
charge on this ring \({dq}=\sigma {d} {A}\)
\({d} {E} z=\frac{{kdqz}}{\left({z}^{2}+{r}^{2}\right)^{3 / 2}}\)
\(E=\int_{0}^{\mathbb{R}} {dE}_{z}=\frac{\sigma}{2 \epsilon_{0}}\left[1-\frac{{z}}{\sqrt{{R}^{2}+{z}^{2}}}\right]\)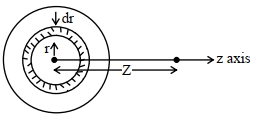
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionદ્વિ ધ્રુવીય ચાકમાત્રાનો એકમ ......... છે.
- 2નીચે બે વિધાનો આપેલા છે.View Solution
વિધાન $-I$ : એક બિંદુવત વિદ્યુતભારને વિદ્યુતક્ષેત્રમાં લાવવામાં આવે છે. જો વિદ્યુતભાર ધન હશે તો વિદ્યુતભારની નજીકના બિંદુ આગળ વિદ્યુતક્ષેત્ર વધશે.
વિધાન $-II$ : એક વિદ્યુત દ્વિ-ધ્રુવીને અસમાન (અનિયમિત) વિદ્યુત ક્ષેત્રમાં મૂકવામાં આવેછે. દ્વિ-ધ્રુવી પર સમાસ (પરિણામી) બળ કદાપિ શૂન્ય નહી થાય.
નીચે આપેલા વિકલ્પોમાંથી સાચો વિકલ્પ પસંદ કરો.
- 3ડાઈપોલ માટે પ્રત્યેક વિદ્યુતભારની કિંમત $10^{-10} \,st\, C$ અને તેમના વચ્ચેનું અંતર $1\,\mathop A\limits^o $ હોય તો તેની ડાઈપોલની ચાકમાત્રા ........ છે.View Solution
- 4$5\,\mu C$,$0.16\,\mu C$ અને $0.3\,\mu C$ નાં ત્રણ બિંદુવત્ત વીજભારો, કાટકોણ ત્રિકોણ કે જેની બાજુઓ $A B=3\,cm , B C=3 \sqrt{2}\,cm $ અને $C A=3\,cm$ અને $A$ એ કાટકોણ હોય તેના શિરોબિંદુ $A, B, C$ પર મૂકવામાં આવેલ છે. $A$ ઉપર રહેલો વિદ્યુતભાર બાકીના વિદ્યુતભારોને કારણે $.........N$ જેટલું સ્થિત વિદ્યુતકીય બળ અનુભવશે.View Solution
- 5View Solutionજ્યારે સુવાહક સાબુના ફિણને ઋણભારીત કરવામાં આવે તો
- 6$8$ $\mu g$ દળ અને $39.2 \times {10^{ - 10}}$ વિદ્યુતભાર ધરાવતા ગોળાથી બનાવેલ સાદા લોલક પર સમક્ષિતિજ દિશામાં $20 \times {10^3}\ volt/meter$ વિદ્યુતક્ષેત્ર લગાવતાં,દોરી શિરોલંબ સાથે કેટલા .......$^o$ નો ખૂણો બનાવે?View Solution
- 7એક બંધ પૃષ્ઠની અંદર અને બહાર જતું વિદ્યુત ફલ્કસ ${\varphi _1}$ અને ${\varphi _2}$ છે.તો પૃષ્ઠની અંદર વિદ્યુતભાર કેટલો હશે?View Solution
- 8વિદ્યુતભારિત કરેલા તેલના ટીપાને $3 \times10^{4}\; V / m$ ના સમાન ક્ષેત્રમાં એવી રીતે મૂકવામાં આવે છે કે જેથી તે નીચે પણ ના પડે અને ઉપર પણ ના જાય. ટીપાં પરનો વિદ્યુતભાર ($\times10^{-18}\;C$ માં) કેટલો હશે?View Solution
(વિદ્યુતભારનું દળ $=9.9 \times 10^{-15} kg$ અને $g=10 m/s ^{2}$ લો)
- 9$+8q$ અને $-2q$ બિંદુવત વિદ્યુતભારો $x = 0$ અને $x = L$ પાસે મૂકેલાં છે. તો $X -$ અક્ષ પરના કયા બિંદુ આગળ પરિણામી વિદ્યુતક્ષેત્રની તીવ્રતા શૂન્ય થશે?View Solution
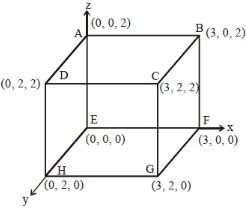
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે બોક્સમાથી $\overrightarrow{\mathrm{E}}=4 \mathrm{x} \hat{\mathrm{i}}-\left(\mathrm{y}^{2}+1\right) \hat{\mathrm{j}}\; \mathrm{N} / \mathrm{C}$ જેટલું વિદ્યુતક્ષેત્ર પસાર થાય છે $A B C D$ અને $BCGF$ સપાટીમાંથી પસાર થતું ફ્લક્સ $\phi_{I}$ અને $\phi_{\mathrm{II}}$ હોય તો તેમનો તફાવત $\phi_{\mathrm{I}}-\phi_{\mathrm{II}}$ ($\mathrm{Nm}^{2} / \mathrm{C}$ માં) કેટલો મળે?View Solution