સમાન બાજુ ધરાવતાં અષ્ટકોણ $ABCDEFGH$ માટે $\overrightarrow{ AB }+\overrightarrow{ AC }+\overrightarrow{ AD }+\overrightarrow{ AE }+\overrightarrow{ AF }+\overrightarrow{ AG }+\overrightarrow{ AH }$ નો સરવાળો કેટલો હશે, જો $\overrightarrow{ AO }=2 \hat{ i }+3 \hat{ j }-4 \hat{ k }$ હોય ?
JEE MAIN 2021, Diffcult
Download our app for free and get started
b
We know,
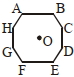
We know,
\(\because \overrightarrow{ OA }+\overrightarrow{ OB }+\overrightarrow{ OC }+\overrightarrow{ OD }+\overrightarrow{ OE }+\overrightarrow{ OF }+\overrightarrow{ OG }+\overrightarrow{ OH }=\overrightarrow{0}\)
By triangle law of vector addition, we can write
\(\overrightarrow{ AB }=\overrightarrow{ AO }+\overrightarrow{ OB } ; \overrightarrow{ AC }=\overrightarrow{ AO }+\overrightarrow{ OC }\)
\(\overrightarrow{ AD }=\overrightarrow{ AO }+\overrightarrow{ OD } ; \overrightarrow{ AE }=\overrightarrow{ A O }+\overrightarrow{ OE }\)
\(\overrightarrow{ AF }=\overrightarrow{ AO }+\overrightarrow{ OF } \quad ; \overrightarrow{ AG }=\overrightarrow{ AO }+\overrightarrow{ OG }\)
\(\overrightarrow{ AH }=\overrightarrow{ A O }+\overrightarrow{ OH }\)
Now
\(\overrightarrow{ AB }+\overrightarrow{ AC }+\overrightarrow{ AD }+\overrightarrow{ AE }+\overrightarrow{ AF }+\overrightarrow{ AG }+\overrightarrow{ AH }\)
\(=(7 \overrightarrow{ AO })+\overrightarrow{ OB }+\overrightarrow{ OC }+\overrightarrow{ OD }+\overrightarrow{ OE }+\overrightarrow{ OF }+\overrightarrow{ OG }+\overrightarrow{ OH }\)
\(=(7 \overrightarrow{ AO })+\overrightarrow{0}-\overrightarrow{ OA }\)
\(=(7 \overrightarrow{ AO })+\overrightarrow{ AO }\)
\(=8 \overrightarrow{ A O }=8(2 \hat{ i }+3 \hat{ j }-4 \hat{ k })\)
\(=16 \hat{i}+24 \hat{j}-32 \hat{k}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\vec{A}$ એવી સદિશ રાશિ છે કે $|\vec{A}|=$ અશૂન્ય અચળાંક છે. નીચેનામાંથી ક્યું સમીકરણ $\vec{A}$ માટે સાચું છે?View Solution
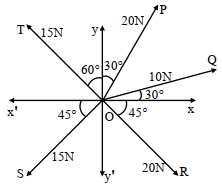
- 2$\overrightarrow{O P}, \overrightarrow{O Q}, \overrightarrow{O R}, \overrightarrow{O S}$ અને $\overrightarrow{{OT}}$ નું પરિણામી બળ લગભગ $\ldots \ldots {N}$ જેટલું થાય.View Solution
[$\sqrt{3}=1.7, \sqrt{2}=1.4$ , $\hat{{i}}$ અને $\hat{{j}}$ એ ${x}, {y}$ અક્ષની દિશાના એકમ સદીશ છે.$]$
- 3જો $ |\,\vec A + \vec B\,|\, = \,|\,\vec A\,| + |\,\vec B\,| $ હોય, તો $ \vec A $ અને $ \vec B $ વચ્ચેનો ખૂણો ....... $^o$ હશે.View Solution
- 4$\overrightarrow A + \overrightarrow B + \overrightarrow C= 0$ આપેલ છે. ત્રણ સદિશ પૈકી બે સદિશોનું મૂલ્ય સમાન છે. અને ત્રીજા સદિશનું મૂલ્ય $\sqrt 2 $ ગણું કે જે બે સમાન મૂલ્ય સિવાયનું છે. તો સદિશો વચ્ચેના ખૂણાઓ શું હશે ?View Solution
- 5જો સદિશ $ \overrightarrow A = 2\hat i + 4\hat j - 5\hat k $ ,હોય તો સદીશનો દિશાકીય cosine કેટલો થાય?View Solution
- 6$10 \,N$ મૂલ્ય વાળા પાંચ સમાન બળોને એક જ સમતલ માં એક બિંદુ પર લગાવવામાં આવે છે.જો તેઓ ની વચ્ચેનો ખૂણો સમાન હોય તો પરિણામી બળ ............. $\mathrm{N}$ થાય?View Solution
- 7જો $\vec P = \vec Q$ હોય તો તેના માટે નીચેનામાંથી શું સાચું નથી?View Solution
- 8એક ઓરડાના પરિમાણ $ 10\,m \times 12\,m \times 14\,m. $ હોય તો એક પતંગિયું એક ખૂણેથી,વિકર્ણના સામેના ખૂણે જાય, તો તેના દ્વારા થયેલા સ્થાનાંતરનું મુલ્ય કેટલા......... $m$ હશે?View Solution
- 9સદિશ $\mathop A\limits^ \to \,$ અને $ \,\mathop B\limits^ \to $ x-અક્ષની સાપેક્ષે અનુક્રમે $20^0$ અને $110^0$ ખૂણો બનાવે છે. આ સદિશોનું મૂલ્ય અનુક્રમે $5 m$ અને $12 m$ છેતો તેના પરિણામી સદીશે x-અક્ષ સાથે રચાતા ખૂણાનું મૂલ્ય ..... મળેે.View Solution
- 10View Solutionશું બે સદિશોનો પરિણામી સદિશ શૂન્ય થઈ શકે?