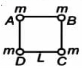
(d)
Work done by the gravitational force acting on the particle \(D\) during its movement
\(=-\Delta U\)
\(=-\left(U_{\text {final }}-U_{\text {initial }}\right)\)
\(=U_{\text {initial }}-U_{\text {final }}\)
Now, when the particle is at infinity, \(U=0\)
\(\Rightarrow U_{\text {final }}=0\)
\(\Rightarrow \text { Work done }=U_{\text {initial }}\)
\(U_{\text {initial }}=-\frac{G m^2}{L}-\frac{G m^2}{L}-\frac{G m^2}{\sqrt{2} L}\)
\(=-\frac{G m^2}{L}\left(2+\frac{1}{\sqrt{2}}\right)\)
\(=-\frac{G m^2}{L}\left(\frac{2 \sqrt{2}+1}{\sqrt{2}}\right)\)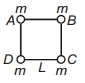
Download our appand get started for free
Similar Questions
- 1ગ્રહ $ A $ પર નો ગુરુત્વપ્રવેગ એ ગ્રહ $B$ ના ગુરુત્વપ્રવેગ કરતાં $9$ ગણો છે. એક માણસ $ A$ ની સપાટી પર $2\,m$ નો કૂદકો મારે છે. તો તે જ વ્યક્તિ ગ્રહ $B$ પર કેટલો ઊંચો ($m$ માં) કૂદકો મારી શકે?View Solution
- 2પૃથ્વીની સપાટીથી કેટલા $km$ ઊંચાઈએ ગુરુત્વ પ્રવેગનું મુલ્ય પૃથ્વીની સપાટીથી $10 \,km$ ઊંડાઈ જેટલો થાય?View Solution
- 3$1\,kg$ દળ ધરાવતા પદાર્થ માટે તેને પૃથ્વીની સપાટીથી પૃથ્વીની ત્રિજ્યા કરતાં ત્રણ ગણી ઊંચાઈએ લઈ જતાં તેણે પ્રાપ્ત કરેલી સ્થિતિ ઊર્જા $......MJ$ થશે.( $g =10 ms ^{-2}$ અને પૃથ્વીની ત્રિજ્યા = $6400\,km )$View Solution
- 4પૃથ્વી પરથી પદાર્થની નિષ્ક્રમણ ઝડપ $11.2 \,km / s$ છે. ધારો કે પૃથ્વીનું દળ અને ત્રિજ્યા ચંદ્રનાં દળ અને ત્રિજ્યા કરતાં $81$ અને $4$ ગણી છે. તો ચંદ્રની સપાટી પરથી નિષ્કમણ વેગ $km / s$ માં શું હશે ?View Solution
- 5નીચે બે વિધાનો આપેલા છે : એકને કથન $A$ અને બીજાને કારણ $R$ વડે દર્શાવેલ છે.View Solution
કથન $A$ : જ્યારે આપણે ધ્રુવથી વિષુવવૃત્ત તરફ ગતિ કરીએ છીએ, પૃથ્વીનો ગુરુત્વાકર્ષી પ્રવેગની દિશા સહેજ વિચલિત થયા વગર, હંમેશા પૃથ્વીના કેન્દ્ર તરફ જ રહે છે.
કારણ $R$ : વચ્યેના કોઈ અક્ષાંસ (Latitude) આગળ, પૃથ્વીની ગુરુત્વાકર્ષી પ્રવેગની દિશા પૃથ્વીના કેન્દ્રથી વિચલિત થાય છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 6સૂર્યની આજુબાજુ ભ્રમણ કરતાં ગ્રહની કોણીય ઝડપ ($\omega$) અને અંતર $(r)$ હોય,તો ગ્રહનો ક્ષેત્રીય વેગ...View Solution
- 7ધારોકે એક હળવો ગ્રહ એક બહુ વજનદાર તારાની ફરતે $R$ ત્રિજ્યાની કક્ષામાં $T $ આવર્તકાળથી ફરે છે.તારા અને ગ્રહ વચ્ચેનું ગુરુત્વાકર્ષી બળ $R^{-5\over 2}$ ના સમપ્રમાણમાં હોય તો $T^2$ કોના સમપ્રમાણ માં હોય ?View Solution
- 8પૃથ્વીને અચળ ઘનતા ધરાવતો ગોળો માનવામાં આવે તો પૃથ્વીની અંદર કેન્દ્રથી $r$ અંતરે ગુરુત્વપ્રવેગ કોના સમપ્રમાણમાં હશે?View Solution
- 9પૃથ્વીની સપાટી પર ધ્રુવ પાસે ગુરુત્વપ્રવેગનું મૂલ્ય $g$ અને ધુવમાંથી પસાર થતી અક્ષને અનુલક્ષીને કોણીય ઝડપ $\omega$ છે. એક પદાર્થનું વજન વિષુવવૃત પર અને ધુવથી $h$ ઊંચાઈ પર સ્પ્રિંગ બેલેન્સ વડે માપવામાં આવે છે.જો બંને સ્થાને વજન સમાન મળતું હોય તો ઊંચાઈ $h$ કેટલી હશે? $( h << R ,$ જ્યાં $R$ એ પૃથ્વીની ત્રિજ્યા છે)View Solution
- 10બે ગ્રહ જેના વ્યાસ નો ગુણોત્તર $4:1$ અને ઘનતાનો ગુણોત્તર $1:2$ હોય તો તેના ગુરુત્વ પ્રવેગ નો ગુણોત્તર કેટલો થાય?View Solution
