As the permittivity of dielectric varies linearly from \(\varepsilon_{1}\) at one plate to \(\varepsilon_{2}\) at the other, it is governed by equation,
\(k=\left(\frac{\varepsilon_{2}-\varepsilon_{1}}{d}\right) x+\varepsilon_{1}\)
Consider a small element of thickness \(d x\) at a distance \(x\) from plate. Then,
\(d V=\frac{E_{0}}{k} d x \Rightarrow \int_{0}^{V} d V=\int_{0}^{d} \frac{\sigma}{\varepsilon_{0}} \frac{1}{\left(\frac{c_{2}-\varepsilon_{1}}{d}\right) x+\varepsilon_{1}} d x\)
\(V=\frac{d \sigma}{\varepsilon_{0}\left(\varepsilon_{2}-\varepsilon_{1}\right)} \ln \left(\frac{\varepsilon_{2}}{\varepsilon_{1}}\right)\)
\(Q=C V \Rightarrow C=\frac{Q}{V}=\frac{\sigma A}{\frac{d \sigma}{\varepsilon_{0}\left(\varepsilon_{2}-\varepsilon_{1}\right)} \ln \left(\frac{\varepsilon_{2}}{\varepsilon_{1}}\right)}=\frac{\varepsilon_{0}\left(\varepsilon_{2}-\varepsilon_{1}\right) A}{d \ln \left(\frac{\varepsilon_{2}}{\varepsilon_{1}}\right)}\)
Download our appand get started for free
Similar Questions
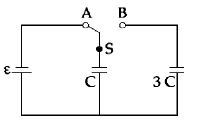
- 1આકૃતિમાં બતાવ્યા પ્રમાણે કળ $S$ ને સ્થિતિ $A$ થી સ્થિતિ $B$ માં ફેરવ્યા બાદ કેપેસિટર $C$ અને કુલ વિદ્યુત ભાર $Q$ ના પદોમાં આ પરિપથમાં કેટલી ઊર્જાનો વ્યય થશે?View Solution
- 2$Millikan's$ ના તેલના ટીપાના પ્રયોગમાં $Q$ વિદ્યુતભારને બે પ્લેટો વચ્ચે $2400\, V$ ના વિદ્યુતસ્થીતીમાનના તફાવત હેઠળ સ્થીર રાખેલ છે બીજા અડધી ત્રિજ્યા ધરાવતા ટીપાંને સ્થીર રાખવા માટે $600\,V$ નો વિદ્યુત સ્થીતીમાનનો જરૂરી છે તો બીજા ટીપા પરનો વિદ્યુતભાર....View Solution
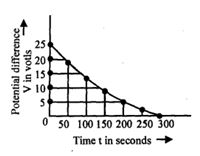
- 3આકૃતિ $RC$ પરિપથમાં કેપેસિટરના ડિસ્ચાર્જિંગનો પ્રાયોગિક ગ્રાફ દર્શાવે છે. તો આ પરિપથનો સમય અચળાંક કયા સમયગાળાની વચ્ચે આવેલ છે ?View Solution
- 4ત્રણ કેપેસીટર દરેક $C$ કેપેસીટન્સ ધરાવતા તથા $V$ બ્રેક ડાઉન વોલ્ટેજ ધરાવતા કેપેસીટરોને શ્રેણીમાં જોડેલ હોય તો સમતુલ કેપેસીટન્સ તથા બેકડાઉન વોલ્ટેજ શોધો ?View Solution
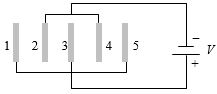
- 5આપેલ તંત્રમાં દરેક પ્લેટનું ક્ષેત્રફળ $A$ અને બે પ્લેટ વચ્ચેનું અંતર $d$ છે,તો પ્લેટ $1$ અને $4$ પર વિદ્યુતભાર કેટલો થશે?View Solution
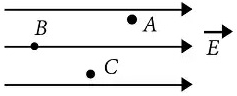
- 6એક સમાન વિદ્યુતક્ષેત્રમાં $A,B$ અને $C$ ત્રણ બિંદુઓ છે.વિદ્યુતસ્થિતિમાન ......View Solution
- 7વિદ્યુતક્ષેત્ર $E$ માં વિદ્યુતક્ષેત્રની દિશામાં $p$ દ્વિ ધ્રુવીય ચાકમાત્રા વાળી ડાઈપોલ $\theta $ ખૂણો ભ્રમણ કરે છે. તે દરમિયાન ડાઈપોલ પર થતું કાર્ય ...... છે.View Solution
- 8એક $2500 \,\mu F$ વાળા કેપિસિટરને $12 \,V.d.c.\, 1 \,k\Omega$ ઉદગમ દ્વારા અવરોધમાંથી કરેલ છે. $5$ સેકન્ડ પછી કેપેસિટર વચ્ચેનો વોલ્ટેજ ..... $volt$ છે.View Solution
- 9$1$ જેટલો ડાઈઈલેક્ટ્રીક અચળાંક ધરાવતા અવાહકથી બનેલો સાધન ગોળો નિયમિત રીતે ચાર્જ કરવામાં આવ્યો છે. જો અનંત અંતરે સ્થિતિમાન શૂન્ય છે તેમ ધારી લઈએ તો તેની સપાટીએ $V$ સ્થિતિમાન શૂન્ય લઈએ તો તેના કેન્દ્ર પર કેટલો સ્થિતિમાન મળશે?View Solution
- 10$5\, km$ પહોળાઈ અને $5\, km$ લંબાઈ ધરાવતો એક વિશાળ જળવાદળ છે. તેનું તળિયું (પાયો અહી દર્શાવ્યા પ્રમાણે પૃથ્વીની સપાટીથી $1\, km$ ઉપર છે. ડાઈ ઈલેકટ્રીક તરીકે હવાના માધ્યમ સાથે પૃથ્વીની સપાટી અને વાદળને સમાંતર પ્લેટ કેપેસિટર હોય તેમ ધારો તો વાદળ અને પૃથ્વી સપાટી સંયોજનનું કેપેસિટન્સ........$\mu F$ માં શોધો.View Solution

