(પદાર્થની સાપેક્ષ પરમીએબિલિટી $50$ છે)
\(\rho=200\, \Omega {m}\)
\({C}=2 \times 10^{-12}\, {F}\)
\({V}=40\, {V}\)
\({K}=56\)
\(C =\frac{ K \varepsilon_0 A }{ d }\) (\(K\) is the dielectric constant or relative permittivity) and
\(R =\frac{\rho d }{ A }\)
Now, charge will be discharged through the resistance between the plates.
Now, time constant ( \(( T )\) of discharging,
\(\tau= RC =\frac{\rho d }{ A } \times \frac{ K \varepsilon_0 A }{ d }\)
\(\tau=\rho K \varepsilon_0\)
For a given R-C circuit, the discharged current is given by
\(i =\frac{ Q }{ RC } e ^{-\frac{ t }{ RC }}\)
\(i =\frac{ Q }{ pK \varepsilon_0} e ^{-\frac{ t }{ pK \varepsilon_0}}\)
The above discharge current is the leakage current,
\(i _{\text {leakage }}=\frac{ Q }{\rho K \varepsilon_0} e ^{-\frac{ t }{\rho K \varepsilon_0}}\)
Maximum leakage current,
\(\left( i _0\right)_{\text {leakage }} =\frac{ Q }{\rho K \varepsilon_0}=\frac{ CV }{\rho K \varepsilon_0}\)
\(=\frac{2 \times 10^{-12} \times 40}{200 \times 50 \times 8.85 \times 10^{-12}}\)
\(=903 \mu A =0.9 mA\)
\(\left( i _0\right)_{\text {leakage }} =0.9 \;mA\)
Download our appand get started for free
Similar Questions
- 1$m$ દળ અને $q$ વિદ્યુતભાર ધરાવતા કણને સ્થિર સ્થિતિમાં $E$ વિદ્યુતક્ષેત્રમાં મુકીને તેને મુક્ત કરવામાં આવે છે. $y$ અંતર કાપ્યા પછી કણની ગતિઊર્જા કેટલી થાય?View Solution
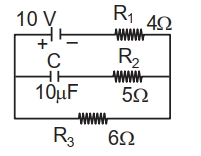
- 2નીચે દોરેલ વિદ્યુત પરિપથમાં સંઘારકમાં સંગ્રહિત વિદ્યુતભાર__________$\mu \mathrm{C}$હશે.View Solution
- 3$\vec p$ મોમેન્ટ ધરાવતી એક વિદ્યુત ડાઇપોલને વિદ્યુતક્ષેત્ર $\vec E$ ની દિશામાં મૂકેલો છે.આ ડાઇપોલને $90 ^o $ ના કોણે ભ્રમણ કરાવવા માટે કેટલું કાર્ય કરવું પડે?View Solution
- 4$m$ દળ અને $+e$ વિદ્યુતભાર ધરાવતા કણે $v$ વેગથી $Ze$ વિદ્યુતભાર ધરાવતાં પદાર્થ તરફ ફેંકતા કેટલો નજીક જશે? $(Z>0) $View Solution
- 5$\alpha-$કણ અને એક પ્રોટોનને સમાન સ્થિતિમાનના તફાવતથી વિરામ સ્થિતિમાંથી પ્રવેગિત કરવામાં આવે છે. બંને દ્વારા પ્રાપ્ત કરેલ રેખીય વેગમાનોનો ગુણોત્તર $..........$ થશે.View Solution
- 6View Solutionજવલનશીલ પ્રવાહી લઈ જતા વાહનમાં સામાન્ય રીતે જમીનને અડકે તેવી ધાતુની સાંકળ રાખવામાં આવે છે.
- 7$20\ \mu F$ કેપેસિટરન્સના કેપેસિટરમાં પ્લેટો વચ્ચેનું અંતર $2\ mm$ છે. જો $1\ mm$ પહોળાઈ અને $2$ ડાય-ઈલેકટ્રીક અચળાંક ધરાવતા ડાય-ઈલેકટ્રીક ચોસલાને પ્લેટોની વચ્ચે દાખલ કરવામાં આવે, તો નવું કેપેસિટન્સ.....$\mu F$View Solution
- 8બે ધાત્વીય તક્તિમાં એક સમાંતર પ્લેટ સંધારક રચે છે. બે પ્લટો વચ્યેનું અંતર ' $d$ ' છે. સમાન ક્ષેત્રફળ ધરાવતી અને $\frac{d}{2}$ જેટલી જાડાઈ ધરાવતી ધાતુનાં પૃષ્ઠની પ્લેટોની વચ્યે દાખલ કરવામાં આવે છે. આ બંને કિસ્સા (એટલે કે ધાતુના પૃષ્ઠ સાથે અને ધાતુ પૃષ્ઠ વગર) માટે સંધારકતાનો ગુણોત્તર કેટલી થશે $?$View Solution
- 9આઠ સમાન વિદ્યુતભારિત ટીપાઓ ભેગા થઈને એક મોટા ટીપાની રચના કરે છે. જો દરેક ટીપાનું સ્થિતિમાન $10\ V$ હોય તો મોટા ટીપાનું સ્થિતિમાન........$V$ જેટલું થશે ?View Solution
- 10વિદ્યુતભારીત કેપેસિટરની પ્લેટો વચ્ચેની સરેરાશ વિદ્યુતીય ઊર્જા ઘનતા (અહી $q$ = કેપેસિટર પર વિદ્યુતભાર અને $A$= કેપેસિટરની પ્લેટોનું ક્ષેત્રફળ)View Solution
