\(V_{A}=\frac{1}{4 \pi \varepsilon_{0}}\left\{\frac{q_{A}}{a}+\frac{q_{B}}{b}+\frac{q_{C}}{c}\right\}\)
\(=\frac{4 \pi}{4 \pi \varepsilon_{0}}\left\{\frac{a^{2} \sigma}{a}-\frac{b^{2} \sigma}{b}+\frac{c^{2} \sigma}{c}\right\}\)
\({V_{A}=\frac{1}{\varepsilon_{0}}\left\{\frac{a^{2} \sigma}{a}-\frac{b^{2} \sigma}{b}+\frac{c^{2} \sigma}{c}\right\}} \)
\({V_{B}=\frac{1}{\varepsilon_{0}}\left\{\frac{a^{2} \sigma}{b}-\frac{b^{2} \sigma}{b}+\frac{c^{2} \sigma}{c}\right\}}\)
\(V_{C}=\frac{1}{\varepsilon_{0}}\left\{\frac{a^{2} \sigma}{c}-\frac{b^{2} \sigma}{c}+\frac{c^{2} \sigma}{c}\right\}\)
Given \(c=a+b\) If \(a=a, b=2 a\) and \(c=3 a\) for example, as \(c>b>a\)
\({V_{A}=\frac{1}{\varepsilon_{0}}\left\{\frac{a^{2} \sigma}{a}-\frac{4 a^{2} \sigma}{2 a}+\frac{c^{2} \sigma}{c}\right\}} \)
\({V_{B}=\frac{1}{\varepsilon_{0}}\left\{\frac{a^{2} \sigma}{2 a}-\frac{4 a^{2} \sigma}{2 a}+\frac{c^{2} \sigma}{c}\right\}}\)
\(V_{C}=\frac{1}{\varepsilon_{0}}\left\{\frac{a^{2} \sigma}{3 a}-\frac{4 a^{2} \sigma}{3 a}+\frac{c^{2} \sigma}{c}\right\}\)
It can seen by taking out common factors that
\(V_{A}=V_{C}>V_{B} \quad \text { i.e., } \quad V_{A}=V_{C} \neq V_{B}\)
Download our appand get started for free
Similar Questions
- 1$20\,\mu F$ ના કેપેસીટરને $500\;volts$ વડે ચાર્જ કરીને બીજા $10\,\mu F$ કેપેસીટર જેને $200\;volts$ વડે ચાર્જ કરેલ છે તેની સાથે સમાંતરમાં જોડેલ છે. તો બંને વચ્ચેનો સામાન્ય વિદ્યુતસ્થિતિમાન કેટલા $volts$ હશે?View Solution
- 2$200 \,\mu {F}$ ના સમાંતર પ્લેટ કેપેસીટરને $200 \, {V} $ ની બેટરી સાથે જોડેલ છે. બેટરીને જોડેલી રાખીને $2$ ડાઈઈલેક્ટ્રિક અચળાંક ધરાવતા ડાઈઈલેક્ટ્રિકને બે પ્લેટ વચ્ચે દાખલ કરવામાં આવે છે. કેપેસીટરની વિદ્યુતઊર્જામાં થતો ફેરફાર ($J$ માં) કેટલો હશે?View Solution
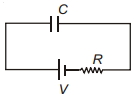
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે, $C$ ક્ષમતા ધરાવતા કેપેસીટર સાથે $R$ જેટલો અવરોધ જોંડલ છે. બેટરી દ્વારા આપવામાં આવતી ઊર્જા કેટલી હશે?View Solution
- 4$1 \,pF$ કેપેસિટન્સની બે પ્લેટ વચ્ચેનું અંતર બમણું કરીને મીણ ભરી દેતાં નવો કેપેસિટન્સ $2\, pF$ થાય છે.તો મીણનો ડાઇઇલેકિટ્રક અચળાંક કેટલો થાય?View Solution
- 5$0.02 \,m$ ની ત્રિજ્યા અને દરેક $5 \mu C$ વીજભાર ધરાવતા યોંસઠ $(64)$ ટીપાં જોડાઈને એક મોટુ ટીપું બનાવે છે. મોટાં ટીપાં અને નાનાં ટીપાંની પૃષ્ઠ ધનતાનો ગુણોત્તર ............... થશે.View Solution
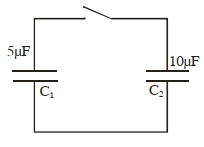
- 6$5 \,\mu F$ ના મૂલ્યના એક સંઘારકને $C _{1} 30 \,V$ ના સ્થિતિમાન થી બેટરી વડે વીજભારિત કરવામાં આવે છે. ત્યારબાદ બેટરીને દૂર કરવામાં આવે છે એ આકૃતિમાં દર્શાવ્યા અનુસાર બીજા $10 \,\mu F$ ના અવિદ્યુતભારિત સંઘારક સાથે જોડવામાં આવે છે. જ્યારે કળ બંધ હોય છે ત્યારે સંધારક વચ્ચે વીજભારનું વહન થાય છે. સંતુલન સમયે, બીજા સંઘારક $C _{2}$ પરનો વિદ્યુતભાર ........... $\mu C$ હશે.View Solution
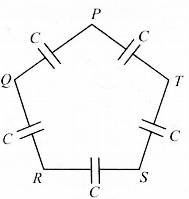
- 7$C$ કેપેસીટન્સ ધરાવતા પાંચ કેપેસીટરને આકૃતિમાં દર્શાવ્યા પ્રમાણે જોડેલા છે. તો $P$ અને $R$ તથા $P$ અને $Q$ વચ્ચેના કેપેસીટન્સનો ગુણોત્તર કેટલો થાય?View Solution
- 8$x-y$ અક્ષોની પ્રણાલીનાં ઉગમ બિંદુ એક $10\,\mu C$ જેટલો ચાર્જ મુકવામાં આવ્યો છે. $(0, a)$ પર $(a, 0)$ બિંદુઓ વચ્ચે કેટલો વિદ્યુત સ્થિતિમાનનો ફરક જોવાં મળશે?View Solution
- 9બે બિંદુવત ડાયપોલ ${\vec P_1}$ અને ${\vec P_2}$ એકબીજાથી $x$ અંતરે અને ${\vec P_1}$ || ${\vec P_2}$ છે.આ બંને ડાયપોલ વચ્ચે કેટલું બળ લાગતું હશે?View Solution
- 10${10^{ - 10}}\,m$ અંતરે રહેલા બે પ્રોટ્રોનને મુકત કરતાં અનંત અંતરે ગતિઊર્જા કેટલી થાય?View Solution
