સમતલીય પોલરઇઝ્ડ વિદ્યુતચુંબકીય તરંગ શૂન્યાવકાશમાં એવી રીતે ગતિ કરે છે કે જેથી $t\, = t_1$ સમયે $z_1$ બિંદુ આગળ તેનું વિદ્યુતક્ષેત્ર શૂન્ય થાય છે. તેની નજીકમાં બીજો શૂન્ય $z_2$ આગળ મળે છે. તો આ વિદ્યુતચુંબકીય તરંગની આવૃતિ કેટલી હશે?
JEE MAIN 2018, Diffcult
Download our app for free and get started
a
Using \(E=E_{0}-e^{j(k z-\omega t)}\)
Using \(E=E_{0}-e^{j(k z-\omega t)}\)
Given, at \(t=t_{1}, z=z_{1}, E=0\)
the next zero that occurs in it's neighborhood is at \(z_{2},\) the frequency of the electromagnetic wave at \(t_{2}\)
\(e^{i\left(k z_{1}-\omega t_{1}\right)}=e^{i\left(k z_{2}-\omega x_{2}\right)}\)
\(k z_{1}-\omega t_{1}=k z_{2}-\omega t_{2}\)
\(\left(t_{2}-t_{1}\right) \omega=k\left(z-z_{1}\right)\)
where \(k=\frac{2 \pi}{\lambda}=2 \pi v\)
\(\left(t_{2}-t_{1}\right)=\frac{2 \pi}{\lambda \times 2 \pi v}\left(z_{2}-z_{1}\right)\)
\(=\frac{1}{x \times v}\left(z_{2}-z_{1}\right)\)
\(\Rightarrow \lambda \times v=\frac{\left(z_{2}-z_{1}\right)}{\left(t_{2}-t_{1}\right)}=C\)
\(\left(t_{2}-t_{1}\right)=\frac{\left(z_{2}-z_{1}\right)}{C}\)
Frequency is \(f \propto \frac{1}{t}\) then \(\frac{1}{\left(t_{2}-t_{1}\right)}=\frac{C}{\left(z_{2}-z_{1}\right)}\)
\(\therefore \text { Frequency, } f=\frac{3 \times 10^{8}}{\left(z_{2}-z_{1}\right)}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionહર્ટ્ઝના પ્રયોગમાં સળિયાઓ ...... તરીકે વર્તેં છે.
- 2ઉદગમ થી નજીકના વિસ્તારમાં વિદ્યુતચુંબકીય તરંગોમાં $\mathop E\limits^ \to $ અને $\mathop B\limits^ \to $ સળિયો ..... દોલનો કરે છે.View Solution
- 3ક્ષ કિરણો અને $\gamma$ - કિરણો બંન્ને વિદ્યુત ચુંબકીય તરંગો છે તેમના માટે નીચેના પૈકી ક્યું વિધાન સાચું છે?View Solution
- 4View Solutionવિધુતચુંબકીય તરંગમાં સૌથી નાની તરંગ લંબાઇ નીચેનામાંથી કોની છે ?
- 5વિદ્યુતચુંબકીય તરંગ પ્રસરણને લગતા નીચે આપેલા વિદ્યાનોમાંથી સાચું વિધાન પસંદ કરો.View Solution
$(A)$ સમતલ વિદ્યુતચુંબકીય તરંગમાં વિદ્યુતક્ષેત્ર અને ચુંબકીય ક્ષેત્ર એકબીજાના લંબ હોવા જોઈએ અને પ્રસરણની દિશા વિદ્યુત ક્ષેત્ર અથવા ચુંબકીય ક્ષેત્રની દિશામાં હોવી જોઈએ.
$(B)$ વિદ્યુત યુંબકીય તરંગમાં ઊર્જા, વિદ્યુત અને ચુંબકીય ક્ષેત્રો વચ્ચે સરખા પ્રમાણમાં વહેંચાયેલી હોય છે.
$(C)$ વિદ્યુતક્ષેત્ર અને ચુંબકીય ક્ષેત્ર એકબીજાને સમાંતર અને પ્રસરણ દિશાને લંબ હોય છે.
$(D)$ વિદ્યુતક્ષેત્ર, ચુંબકીય ક્ષેત્ર અને પ્રસરણ દિશા એકબીજાને લંબ હોય છે.
$(E)$ ચુંબકીયક્ષેત્રના મૂલ્યનો અને વિદ્યુતક્ષેત્રના મૂલ્યનો ગુણોત્તર પ્રકાશની ઝડ૫ આપે છે.
નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરે.
- 6View Solutionનીચે પૈકી કયા કિરણની આવૃતિ મહત્તમ હશે?
- 7નીચે બે વિધાનો આપેલા છેView Solution
વિધાન $1$:- અવકાશમાં ગતિ કરતા વિદ્યુત ચુંબકીય તરંગો પોતાની સાથે ઊર્જાનું વહન કરે છે. જેમાં વિદ્યુત ક્ષેત્ર અને ચુંબકીય ક્ષેત્રના સ્વરૂપમાં સમાન ઉર્જ આવેલી હોય છે. વિધાન
$2$:- જયારે વિદ્યુત ચુંબકીય તરંગો કોઈ સપાટી પર આપાત થાય ત્યારે તે સપાટી પર દબાણુ લગાડે છે.
- 8અચુંબકીય ડાઈઇલેક્ટ્રિક માધ્યમમાં સમતલીય વિદ્યુતચુંબકીય તરંગ માટે વિદ્યુતક્ષેત્ર $\vec E\, = \,{\vec E_0}\,(4 \times {10^{ - 7}}\,x - 50t)$ મુજબ આપવામાં આવે છે, જ્યાં અંતર મીટરમાં અને સમય સેકન્ડમાં છે. તો આ માધ્યમનો ડાઈઇલેક્ટ્રિક અચળાંક કેટલો હશે?View Solution
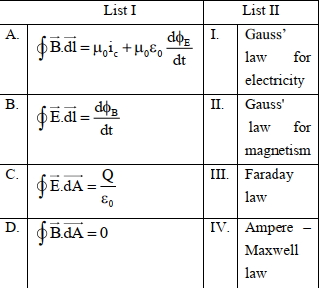
- 9સૂચિ $I$ સાથે સૂચિ $II$ને જોડો :View Solution
નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરોઃ
- 10વિજ ચુંબકીય તરંગોની સૂચિ $I$ સાથે અનુષાંગિત તરંગલંબાઈની સૂચિ $II$ ને યોગ્ય રીતે જોડો.View Solution
સૂચિ $I$ સૂચિ $II$ $(A)$ માઈક્રોતરંગો $(I)$ $400\,nm$ થી $1\,nm$ $(B)$ પારજાંબલી $(II)$ $1\,nm$ થી $10^{-3}\,nm$ $(C)$ $X-$કિરણો $(III)$ $1\,mn$ થી $700\,nm$ $(D)$ પારરકત $(IV)$ $0.1\,m$ થી $1\,mm$ નીચે આપેલા વિકલ્પોમાથી સાચો ઉત્તર પસંદ કરો.