$A ( g ) \rightleftharpoons B ( g )+\frac{1}{2} C ( g )$
વિયોજન અચળાંક $K,$ વિયોજન અંશ $(\alpha)$ અને સંતુલન દ્રાવણ $( p )$ વચ્ચેનો સંબંધ નીચેના વડે દર્શાવેલ છે.
\(\quad\quad\quad\quad A ( g ) \rightleftharpoons B ( g )+\frac{1}{2} C ( g )\)
Initial \(:\quad \, P _{ i } \quad\quad\quad0\quad\quad\quad 0\)
At eq.\(: \,P _{ i }(1-\alpha)\quad P _{ i } \cdot \alpha \quad P _{ i } \frac{\alpha}{2}\)
Now, equilibrium pressure (p),
\(P = P _{ i } \times\left(1+\frac{\alpha}{2}\right)\)
\(\therefore P _{ A }=\left(\frac{1-\alpha}{1+\frac{\alpha}{2}}\right) P\)
\(P _{ B }=\left(\frac{\alpha}{1+\frac{\alpha}{2}}\right) P\)
\(P _{ C }=\left(\frac{\frac{\alpha}{2}}{1+\frac{\alpha}{2}}\right) P\)
\(\therefore K =\frac{ P _{ c }^{\frac{1}{2}} \times P _{ B }}{ P _{ A }}\)
\(K =\frac{\alpha^{\frac{3}{2}} p ^{\frac{1}{2}}}{(2+\alpha)^{\frac{1}{2}}(1-\alpha)}\)
Download our appand get started for free
Similar Questions
- 1ધન લેડ નાઈટ્રેટ $1\,liter$ પાણીમાં ઓગાળેલ છે દ્રાવણ $100.15^{\circ}\,C$ પર ઉકળતું માલૂમ પડે છે. પરિણામી દ્રાવણમાં જ્યારે $0.2\,mol\,NaCl$ ઉમેરવામાં આવે છે ત્યારે, દ્રાવણ $-0.8^{\circ}\,C$ પર ઠરતું જોવા મળ્યું $298\,K$ પર બનતા $PbCl_2$, નો દ્રાવણ ગૂણાકાર $.........\times 10^{-6}$ છે. (નજીકનો પૂર્ણાંક)View Solution
આપેલ : $K_b=0.5\,K\,kg\,mol ^{-1}$ અને $K _f=1.8\,K\,kg\,mol ^{-1}$ બધાજ કિસ્સાઓમાં મોલાલિટી એ મોલારિટી ને સમાન છે તેમ ધારી લો.
- 2જો $AgCl$ નો દ્રાવ્યતા ગુણાકાર $10^{-10}$ હોય તો $0.001\, M \,NaCl$ માં $AgCl$ ની દ્રાવ્યતા કેટલી થાય છે ?View Solution
- 3View Solutionજલવિભાજનમાં સંયોજન..... છે.
- 4નીચેનામાંથી $KOH$ નાં પાંચ દ્રાવણને બનાવવામાં આવે છે.પ્રથમ $\to$$1$ લીટરમાં $ 0.1$ મોલ, દ્વિતીય $\to$$2$ લીટરમાં $0.2$ મોલ, તૃતિય $\to$$3$ લીટરમાં $0.3$ મોલ, ચતુર્થ $\to$ $4$ લીટરમાં $0.4$ મોલ પાચમું $\to $ $5$ લીટરમાં $0.5$ મોલ, પરિણામી દ્રાવણની $pH$ = .......?View Solution
- 5$50 \,ml.\, 0.05 \,M$ ફોર્મિક એસિડ બનાવવા માટે દ્રાવણ $pH = 4.0$ ઉમેરેલા $0.10 \,M$ સોડિયમ ફોર્મેંટના કેટલા......$ml$ કદની જરૂરી પડે છે ? (એસિડની $pK_a = 3.7$)View Solution
- 6$PbS$ ની દ્રાવ્યતા ગુણાકાર $3.4\times10^{-28}$ જો $[Pb^{+2}] $ $=$ $ 1 \times10^{-2}$ મોલ/લીટર તો $ PbS$ ના અવક્ષેપ મેળવવા માટે ની $ [S^{-2}] $ કેટલી સાંદ્રતા મળે ?View Solution
- 7View Solutionનીચે આપેલા દ્રાવ્યતા વક્ર સાથેના ક્ષારની તત્ત્વયોગમિતી અને દ્રાવ્યતા ગુણાકાર અનુક્રમે જણાવો.
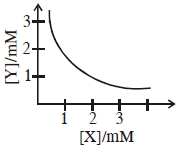
- 8નીચેનામાંથી કોનો વિયોજન અંશ સૌથી વધુ હશે ? તેમાંનું એક $4-$ નાઇટ્રોફિનોલની જલીય દ્રાવણમાં સાંદ્રતા દર્શાવે છે.View Solution
- 9નીચે બતાવેલ બે એસિડ સામેલ નીચેની પ્રક્રિયા ધ્યાનમાં લો: ફોર્મિક એસિડ અને. $HF$View Solution
આ પ્રક્રિયા વિશે નીચેનામાંથી કયું વિધાન સાચું છે
$(A)$ પ્રક્રિયામાં ફોર્મિક એસિડ સૌથી મજબૂત બ્રોન્સ્ટેડ એસિડ છે
$(B)\, HF$ પ્રક્રિયામાં સૌથી મજબૂત બ્રોન્સ્ટેડ એસિડ છે
$(C)\, KF$ પ્રક્રિયા માં સૌથી મજબૂત બ્રોન્સ્ડ બેઇઝ છે
$(D)\, KO_2CH$ પ્રક્રિયા માં સૌથી મજબૂત બ્રોન્સ્ડ બેઇઝ છે
$(E)$ સંતુલન પ્રક્રિયા આપનારાઓની તરફેણ કરે છે
$(F)$ સંતુલન નિપજોની તરફેણ કરે છે
$(G)$ ફોર્મીક એસિડનો નબળો સનયુગ્મ બેઇઝ હોય છે
$(H)\, HF$ નબળો સયુંગ્મ બેઈઝ ધરાવે છે
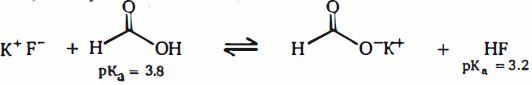
- 10$0.1 \,N \,CH_3COOH$ નો વિયોજન ક્રમ (વિયોજન અચળાંક $= 1 \times 10^{-5}$)View Solution
