સોલર અચળાંક $(S)$ એ સૂર્યના તાપમાન $(T)$ ના ક્યા પ્રમાણમાં આધારિત છે ?
Easy
d
(d)
(d)
Let \(R=\) radius of the sun, \(d=\) distance of the earth from the sun.
Power radiated by the sun \(=\left(4 \pi R^2\right) \sigma T^4=P\).
Energy received per unit area per second normally on the earth
\(= S =\frac{ P }{4 \pi d ^2}=\frac{4 \pi R ^2 \sigma T ^4}{4 \pi d ^2}=\left(\sigma T ^4\right)\left(\frac{ R }{ d }\right)^2=\frac{1}{4} \sigma T ^4\left(\frac{2 R }{ d }\right)^2\)
Angle subtended by the sun at the earth \(=\theta=\frac{2 R}{d}\).
\(\text { or, } S =\frac{\sigma}{4} T ^4 \theta^2\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સૂર્યનું તાપમાન $=6000\, K ,$ સૂર્યની ત્રિજ્યા $=7.2 \times 10^{5}\;km$ પૃથ્વીની ત્રિજ્યા $=6000 \,km$ અને પૃથ્વી અને સૂર્ય વચ્ચેનું અંતર $=15 \times 10^{7}\;km$ કિમી, તો પૃથ્વી પર સૂર્યની તીવ્રતા કેટલી થશે?View Solution
- 2સૂર્યને $T\; K$ તાપમાને $R$ ત્રિજ્યાનાં ગોળા તરીકે ધારતાં, સૂર્યમાંથી પૃથ્વી પર આપાત થતો કુલ ઉત્સર્જન પાવર ગણો. પૃથ્વીનું સૂર્યથી અંતર $r$ લો.View Solution
જ્યાં $r_{0}$ એ પૃથ્વીની ત્રિજ્યા અને $\sigma$ એ સ્ટીફન અચળાંક છે.
- 3કોપર,બ્રાસ અને સ્ટિલના ત્રણ સળિયાને $Y-$ આકારની સંરચના કરવા માટે વેલ્ડિંગ કરવામાં આવે છે.દરેક સળિયાના આડછેદનું ક્ષેત્રફળ $4 $ $cm^2$ છે.કોપર સળિયાના છેડે $100^o $ $C$ તાપમાન જયારે બ્રાસ અને સ્ટિલ સળિયાઓને છેડે $ 0^o $ $C$ તાપમાન જાળવવામાં આવે છે.કોપર,બ્રાસ અને સ્ટિલના સળિયાઓની લંબાઇ અનુક્રમે $46,13 $ અને $12$ cms છે. આ સળિયાઓ છેડેથી જ તાપમાનના સુવાહક છે.જયારે આજુબાજુથી અવાહક છે.કોપર,બ્રાસ અને સ્ટિલની ઉષ્મા વાહકતા અનુક્રમે $0.92,0.26 $ અને $ 0.12 $ $CGS $ એકમમાં છે.કોપર સળિયામાંથી પસાર થતો ઉષ્મા વહન-દર ....... $cal\, s^{-1}$View Solution
- 4અણુના વિસ્ફોટન દરમિયાન ઉત્પન થતી ઉર્જાની મહત્તમ તરંગલંબાઈ $2.93 \times {10^{ - 10}}m$ હોય તો તેણે પ્રાપ્ત કરેલું મહત્તમ તાપમાન કયા ક્રમનું હશે? (વીનનો અચળાંક $=2.93 \times {10^{ - 3}}m - K$View Solution
- 5$0^°C$ તાપમાને રહેલ પદાર્થમાંથી ઉત્સર્જન પાવર $E \,J/sec$ છે,તો $ {273^o}C $ તાપમાને રહેલ તે જ પદાર્થનો ઉત્સર્જન પાવર કેટલો થાય?View Solution
- 6સમાન દ્રવ્યમાંથી બનાવેલ સળિયા નીચે દર્શાવેલ છે .તો $C$ બિંદુનું તાપમાન ..... $^oC$ હશે ?View Solution

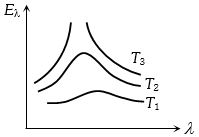
- 7View Solutionસૂર્ય, બલ્બમાં રહેલ ટંગસ્ટન ફિલામેન્ટ અને વેલ્ડિંગ આર્ક માટે વિકિરણ ઉર્જા અને તરંગલંબાઈનો ગ્રાફ આપેલ છે.તો નીચેનામાથી ક્યો વિકલ્પ સાચો પડે?
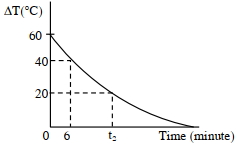
- 8ન્યૂટનનો શીત નિયમ (cooling law) સાબિત કરવાના એક પ્રયોગમાં પાણીનાં અને આસપાસનાં તાપમાનમાં થતા ફેરફાર $(\Delta T)$ અને સમયનો આલેખ દોરવામાં આવેલ છે. પાણીનું પ્રારંભિક તાપમાન $80^{\circ} C$ જેટલું લેવામાં આવે છે. આલેખમાં દર્શાવેલ $t_{2}$ નું મૂલ્ય........થશે.View Solution
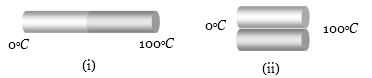
- 9આકૃતિ $(i)$ માં $20$ કેલરી ઉષ્મા $4$ મિનિટમાં પસાર થતી હોય,તો આકૃતિ $(ii)$ માં $20$ કેલરી ઉષ્મા ....... $(\min.)$ સમયમાં પસાર થાય?View Solution
- 10View Solutionઆગની ઉપરની દિશા બાજુ કરતાં વધુ ગરમ લાગે તેનું કારણ ....
