The centripetal force is provided by the magnetic force.
i.e., \(\frac{\mathrm{mv}^{2}}{\mathrm{R}}=\mathrm{qvB}.........(1)\)
where \(m=\) mass of the ion, \(v=\) velocity, \(q=\) charge of ion, \(\mathrm{B}=\) flux density of the magnetic field.
we have, \(\mathrm{v}=\mathrm{R} \omega\)
or \(\omega=\frac{\mathrm{v}}{\mathrm{R}}=\frac{\mathrm{qB}}{\mathrm{m}} \quad(\mathrm{From}(1))\)
Energy of ion is given by,
\(\mathrm{E}=\frac{1}{2} \mathrm{mv}^{2}=\frac{1}{2} \mathrm{m}(\mathrm{R} \omega)^{2}=\frac{1}{2} \mathrm{mR}^{2} \frac{\mathrm{q}^{2} \mathrm{B}^{2}}{\mathrm{m}^{2}}\)
or \(\mathrm{E}=\frac{1}{2} \frac{\mathrm{R}^{2} \mathrm{B}^{2} \mathrm{q}^{2}}{\mathrm{m}}.........(2)\)
If ions are accelerated by electric potential \(V\), the energy attained by ions,
\(E=q V.........(3)\)
From eqns \(( 2)\) and \(( 3)\)
\(\mathrm{qV}=\frac{1}{2} \frac{\mathrm{R}^{2} \mathrm{B}^{2} \mathrm{q}^{2}}{\mathrm{m}}\) or \(\left(\frac{\mathrm{q}}{\mathrm{m}}\right)=\frac{2 \mathrm{V}}{\mathrm{R}^{2} \mathrm{B}^{2}}\)
i.e., \(\left(\frac{\mathrm{q}}{\mathrm{m}}\right) \propto \frac{1}{\mathrm{R}^{2}}(\text { If } \mathrm{V} \text { and } \mathrm{B} \text { are const. })\)
Download our appand get started for free
Similar Questions
- 1કોઇ પરિપથમાં $30\,V $ ની બેટરી અને $40.8 \,ohm $ નો અવરોધ તથા એમિટરને શ્રેણીમાં જોડેલા છે. જો એમિટરના ગૂંચળાનો અવરોધ $480\,ohm$ અને શંટ $20\,ohm$ હોય, તો એમિટરનું અવલોકન ........ $A$View Solution
- 2$L$ લંબાઇ અને $I$ પ્રવાહધારિત તારને એક આંટામાં વાળી દેતાં,કેન્દ્ર પર ચુંબકીયક્ષેત્ર $B$ છે.હવે આ તારને બે આંટામાં વાળતાં કેન્દ્ર આગળ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
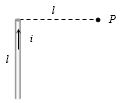
- 3આપેલ આકૃતિ માં $P $ બિંદુએ ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
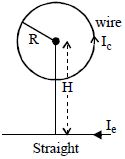
- 4વર્તુળાકાર લૂપ અને સુરેખ તારમાંથી પ્રવાહ $I_c$ અને $I_e$ પસાર થાય છે,બંને એક જ સમતલમાં છે,તો લૂપના કેન્દ્ર પર ચુંબકીય ક્ષેત્ર શૂન્ય કરવા માટે બંન્ને વચ્ચેનું અંતર $H$ ....... .View Solution
- 5ચાર આંટા ધરાવતા એક વર્તુળાકાર ગુંચળામાં વહેંતા પ્રવાહને કારણે તેના કેન્દ્ર આગળ ઉત્પન્ન ચુંબકીય પ્રેરણ $32\,T$ છે. આ ગુંચળાના આંટા ખોલી નાંખવામાં આવે છે અને તેને એક આંટી ધરાવતા વર્તુળાકાર ગૂંચળામાં ફરી વીટાળવામાં આવે છે. ગૂંચળાના કેન્દ્ર આગળ યુંબકીય પ્રેરણ $..........\,T$ થશે.View Solution
- 6એક પ્રોટોન સાયક્લોટ્રોનમાં પ્રવેગિત થાય છે જ્યારે લાગુ પાડેલ ચુંબકીય ક્ષેત્ર $2\,T$ છે. જો વિદ્યુતસ્થિતિમાનનો અસરકારક તફાવત $100\,kV$ હોય તો પ્રોટોનનો $20\,MeV$ ની ગતિઊર્જા પ્રાપ્ત કરવા "$dees$" વચ્ચે કેટલા ભ્રમણ કરવા પડશે ?View Solution
- 7પ્રોટોન,ઇલેક્ટ્રોન અને હીલિયમ ન્યુક્લિયસ પાસે સમાન ઉર્જા છે.તેના સમતલને લંબ ચુંબકીય ક્ષેત્રને કારણે તે વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે.તેમની ત્રિજ્યા અનુક્રમે $r_p, r_e$ અને $r_{He}$ હોય તો....View Solution
- 8એક ગેલ્વેનોમીટર પૂર્ણ આવર્તન માટે $10^{-4}\, A$ જેટલો પ્રવાહ માપી શકે છે. તેને $0 -5\, V$ માપી શકે તેવા વોલ્ટમીટરમાં ફેરવવા માટે શ્રેણીમાં $2\, M\,\Omega $ જેટલો અવરોધ જોડાવો પડે છે.તો આ ગેલ્વેનોમીટરને $0-10\, mA$ પ્રવાહ માપી શકે તેવા એમીટરમાં ફેરવવા માટે કેટલા ......$\Omega $ શંટ અવરોધ જોડવો પડે?View Solution
- 9$\alpha$ કણ અન પ્રોટોન સમાન વેગથી સમાન ચુંબકીય ક્ષેત્રને લંબરૂપે દાખલ થતાં તેના વર્તુળાકાર પથની ત્રિજ્યાનો ગુણોતર ..... .View Solution
- 10$ 2 \times {10^5} $ $m/s$ ના વેગથી ઇલેકટ્રોન ઘન $X$ - દિશામાં ગતિ કરે છે.જો ચુંબકીયક્ષેત્ર $ B = \hat i + 4\hat j - 3\hat k $ હોય,તો તેના પર કેટલું બળ લાગશે?View Solution
