$S(r)\,\, = \,\,\frac{Q}{{\pi {R^4}}}\,r$ એ $R$ ત્રિજ્યા અને કુલ વિદ્યુતભાર $Q$ વાળા એક ધન ગોળાના વિદ્યુતભાર વિતરણની ઘનતા આપે છે. ગોળાના કેન્દ્રથી $r_1$ અંતરે ગોળાની અંદરના બિંદુ $P$ માટે વિદ્યુતક્ષેત્રનું મૂલ્ય ....... છે.
Easy
Download our app for free and get started
a
Consider a differential thickness \(dr\) at a radius \(r\).
Consider a differential thickness \(dr\) at a radius \(r\).
We get the area for this differential thickness as \(dA =4 \pi r ^2 dr\)
Thus we get the electric field at this point as \(dE =\frac{ kdQ }{ r _1^2}\)
or
\(dE =\frac{1}{4 \pi \epsilon_0} \frac{ Qr 4 \pi r ^2 dr }{\pi R ^4 r _1^2}\)
\(E =\frac{ Q }{4 \pi \epsilon_0 r _1^2 \pi R ^4} \int_{ r =0}^{ r } 4 \pi r ^3 dr\)
\(=\frac{ Qr _1^2}{4 \pi \epsilon_0 R ^4}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$9.0\, cm$ ની ધારવાળા એક ઘનાકાર ગોસિયન સપાટીના કેન્દ્ર પર $2.0\; \mu \,C$ વિદ્યુતભાર રહેલો છે. આ સપાટીમાંથી કુલ વિદ્યુત ફલક્સ કેટલું હશે?View Solution
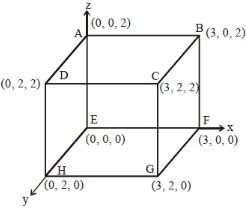
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે બોક્સમાથી $\overrightarrow{\mathrm{E}}=4 \mathrm{x} \hat{\mathrm{i}}-\left(\mathrm{y}^{2}+1\right) \hat{\mathrm{j}}\; \mathrm{N} / \mathrm{C}$ જેટલું વિદ્યુતક્ષેત્ર પસાર થાય છે $A B C D$ અને $BCGF$ સપાટીમાંથી પસાર થતું ફ્લક્સ $\phi_{I}$ અને $\phi_{\mathrm{II}}$ હોય તો તેમનો તફાવત $\phi_{\mathrm{I}}-\phi_{\mathrm{II}}$ ($\mathrm{Nm}^{2} / \mathrm{C}$ માં) કેટલો મળે?View Solution
- 3બે સમાન અને $2\ \mu C$ ના વિરૂદ્ધ વિજભારની બનેલી વિદ્યુત ડાઈપોલ $3\, cm$ અંતરે આવેલી છે. આને $2 \times 10^{+5} N/C$ ના વિદ્યુતક્ષેત્રમાં મૂકેલી હોય તો તેના પર લાગતું મહત્તમ ટોર્ક ..... છે.View Solution
- 4શાંત વાતાવરણમાં વિદ્યુતક્ષેત્ર તીવ્રતા $100 \,V / m$ છે, તો પૃથ્વીની સપાટી પર કુલ વિદ્યુતભાર .............. $C$ છે (પૃથ્વીની ત્રીજ્યા $6400 \,km$ છે.)View Solution
- 5જો $g _{ E }$ અને $g _{ M }$ એ અનુક્રમે પૃથ્વી અને ચંદ્રની સપાટી પર ગુરુત્વપ્રવેગનાં મૂલ્યો હોય અને બંને સપાટ્ટી પર મિલિકાનનો પ્રયોગ કરવામાં આવે તો નીચેના ગુણોત્તરનું મૂલ્ય કેટલું થાય? ચંદ્ર પર વિદ્યુતભાર/પૃથ્વી પર વિદ્યુતભારView Solution
- 6$h$ ઊંચાઈ અને $R$ બેજની ત્રિજ્યા ધરાવતા શંકુને $\vec E$ વિદ્યુતક્ષેત્રમાં એવી રીતે મૂકવામાં આવે છે કે જેથી વિદ્યુતક્ષેત્ર બેજને સમાંતર રહે.તો શંકુમાં દાખલ થતું વિદ્યુત ફ્લક્સ કેટલું હશે?View Solution
- 7સમકેન્દ્રિય ગોળીય કવચ $A$ અને $B $ ની ત્રિજયાઓ $r_A$ અને $r_B(r_B>r_A)$ છે.તેના પર વિદ્યુતભાર $Q_A$ અને $-Q_B(|Q_B|>|Q_A|)$ છે.તો વિદ્યુતક્ષેત્ર વિરુધ્ધ અંતરનો નો આલેખ કેવો થાય?View Solution
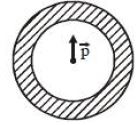
- 8આપેલ આકૃતિમાં દર્શાવેલ પોલા ગોળાની અંદરની ત્રિજ્યા $a$ અને બહારની ત્રિજ્યા $b$ છે જેના પર $Q$ વિદ્યુતભાર છે.તેના કેન્દ્ર પર આકૃતિમાં દર્શાવ્યા પ્રમાણે ડાયપોલ $\vec P$ હોય તો.....View Solution
- 9ખોટું વિધાન પસંદ કરોView Solution
$(a)$ ગાઉસિયન પૃષ્ઠમાં અંદર દાખલ થતી પૃષ્ઠ રેખા ઋણ ફ્લક્સ દર્શાવે છે.
$(b)$ $q$ વિદ્યુતભારને સમઘનના કેન્દ્ર પર મૂકવામાં આવે છે. બધા પૃષ્ઠમાંથી પસાર થતું ફ્લક્સ સમાન હશે.
$(c)$ સમાન વિદ્યુતક્ષેત્રમાં રહેલ શૂન્ય પરિણામી વિદ્યુતભાર ધરાવતા બંધ ગાઉસિયન પૃષ્ઠ સાથે સંકળાયેલ ફ્લક્સ શૂન્ય હોય.
$(d)$ જ્યારે વિદ્યુતક્ષેત્ર ગાઉસિયન પૃષ્ઠને સમાંતર હોય ત્યારે ફ્લક્સ અશૂન્ય હોય.
આપેલ વિકલ્પોમાંથી યોગ્ય વિકલ્પ પસંદ કરો.
- 10બે સમાન ગોળાઓનો વિદ્યુતભાર $+q$ અને $-q$ છે અને તેઓને અમુક અંતરે મૂકેલા છે. તેમના વચ્ચે $F$ બળ લાગે છે. જો બે ગોળાની વચ્ચે $+q$ વિદ્યુતભાર વાળો સમાન ગોળો મૂકવામાં આવે તો તે બળ અનુભવે છે અને જેનું મૂલ્ય અને દિશા ...... છે.View Solution