સરળ આવર્ત ગતિ કરતાં સાદા લોલકનો આવર્તકાળ $T$ છે. જો લોલકની લંબાઇમાં $21\%$ નો વધારો કરવામાં આવે તો વધારેલી લંબાઈના લોલકનાં આવર્તકાળમાં કેટલો વધારો ($\%$) થાય?
AIEEE 2003,AIIMS 2001, Medium
Download our app for free and get started
a
(a) If initial length \({l_1} = 100\) then \({l_2} = 121\)
(a) If initial length \({l_1} = 100\) then \({l_2} = 121\)
By using \(T = 2\pi \sqrt {\frac{l}{g}} \)
\(\Rightarrow \frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{{l_1}}}{{{l_2}}}} \)
Hence, \(\frac{{{T_1}}}{{{T_2}}} = \sqrt {\frac{{100}}{{121}}}\)
\(\Rightarrow {T_2} = 1.1\,{T_1}\)
\(\%\) increase = \(\frac{{{T_2} - {T_1}}}{{{T_1}}} \times 100 = 10\,\% \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક સાદું દોલક $x=0$ ની આસપાસ $a$ કંપવિસ્તાર અને $T$ આવર્તકાળથી સરળ આવર્ત ગતિ કરે છે. $x = \frac{A}{2}$ સ્થાને દોલકની ઝડપ કેટલી હશે?View Solution
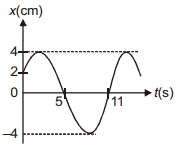
- 2View Solutionનીચેની આકૃતિ, સરળ આવર્તદોલન કરતાં પદાર્થના સ્થાનાંતર સમયનો આલેખ દર્શાવે છે. આ ગતિ દર્શાવતું યોગ્ય સમીકરણ ક્યું છે ?
- 3સરળ આવર્ત ગતિ કરતાં પદાર્થની સ્થિતિઊર્જા સમતોલન સ્થાનથી કંપવિસ્તારના અડધા અંતરે $2.5\, J$ છે,તો કુલઊર્જા કેટલી .... $J$ થાય?View Solution
- 4$X$ અક્ષ પર થતી સરળ આવર્ત ગતિનો કંપવિસ્તાર $4\,cm$ અને આવર્તકાળ $1.2\, sec$ છે,તો $x =2\, cm$ થી $x = + 4\, cm $ જવા અને પાછા આવવા માટે કેટલો સમય .... $\sec$ લાગે?View Solution
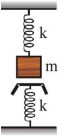
- 5k બળ અચળાંક ધરાવતી સ્પ્રિગ સાથે દળ $m$ જોડવામાં આવેલ છે અને તે મુજબ સપાટી જોડેલ છે.અને તે આકૃતિ મુજબ સપાટી જોડેલ બીજી સ્પ્રિંગને અડે છે. નાના દોલનોનો આવર્તકાળ કેટલો થાય?View Solution
- 6સાદા લોલકનો એક છેડો $10cm$ જેટલી ઉંચાઇએ જઇ શકતો હોય તો તે જયારે તેની મધ્યસ્થ સ્થિતિ એ હોય ત્યારે તેનો વેગ કેટલા .....$m/s$ હોય? $(g = 9.8 m/s^2)$View Solution
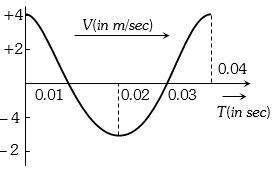
- 7સરળ આવર્તગતિ માટે વેગ વિરુઘ્ઘ સમયનો આલેખ આપેલ છે.તો આવૃત્તિ કેટલી ..... $Hz$ થાય?View Solution
- 8સ. આ.ગ ગતિ કરતા કણની સ્થિતિમાન ઊર્જા $\left(U_x\right)=$View Solution
- 9View Solutionબે કણો એકબીજાની નજીક બે સમાંતર સીધી રેખાઓ સાથે સમાન આવૃતિ અને કંપવિસ્તાર સાથે દોલનો કરે છે. જ્યારે તેમનું સ્થાનાંતર તેમના કંપનવિસ્તારના અડધા હોય છે, ત્યારે તેઓ એકબીજાની વિરુદ્ધ દિશામાં આગળ વધી રહ્યા છે. બે કણોના સમતોલન સ્થાન તેમના માર્ગોને લંબ સીધી રેખા પર છે. તેની વચ્ચેનો કળા તફાવત કેટલો હશે?
- 10$k$ બળ અચળાંક ધરાવતી સ્પ્રિંગના બે ટુકડા કરવામાં આવે છે,મોટા ટુકડાની લંબાઇ નાના ટુકડાની લંબાઇ કરતાં બમણી છે,તો મોટા ટુકડાનો બળ અચળાંક કેટલો થાય?View Solution