સ્થિર પડેલ અસ્થાયી ન્યુક્લિયસ બે ન્યુક્લિયસમાં વિભાજિત થાય છે જેમના વેગનો ગુણોત્તર $8:27$ છે, તો તેમની ત્રિજ્યાનો ગુણોત્તર કેટલો હશે?
JEE MAIN 2018, Diffcult
c
Let heavy nucleus breaks into two nuclei of mass \(m_{1}\) and \(m_{2}\) and move away with velocities \({V}_{1}^1\) and \(V_{2}^2\) respectively.
Let heavy nucleus breaks into two nuclei of mass \(m_{1}\) and \(m_{2}\) and move away with velocities \({V}_{1}^1\) and \(V_{2}^2\) respectively.
According to question, \(\frac{V_{1}}{V_{2}}=\frac{8}{27}\) \(m_{1} V_{1}=m_{2} V_{2}\) (Law of momentum conservation)
\(\Rightarrow\) \(\frac{{{m_1}}}{{{m_2}}} = \frac{{{V_2}}}{{{V_1}}} = \frac{{27}}{8}\)
\(\rho \times \frac{4}{3}\pi R_1^3\) \(\left( {\because {\text{ density }}\rho = \frac{{{\text{ mass }}}}{{{\text{ volume }}}}} \right)\)
\(\rho \times \frac{4}{3}\pi R_2^3\)
\( \Rightarrow \left( {\frac{{{R_1}}}{{{R_2}}}} \right) = \) \({\left( {\frac{{27}}{8}} \right)^{\frac{1}{3}}} = {\left( {\frac{3}{2}} \right)^{3 \times \frac{1}{3}}}\)
\(\therefore \frac{R_{1}}{R_{2}}=\frac{3}{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1રેડિયો એક્ટિવ નમૂનાની એક્ટિવીટી $ t = 0 $ સમયે $9750$ કાઉન્ટસ/મિનિટ $t= 5$ મિનિટે $975$ કાઉન્ટસ/મિનિટ મળે છે. ક્ષય અચળાંક ..........$ min^{-1}$ થશે.View Solution
- 2View Solutionપ્રોટોન નું ન્યૂટ્રોનમાં ક્ષય થાય
- 3ભારે ન્યુક્લિયસ $\frac{N}{P}$ ની કોઈપણ કિંમત માટે અસ્થાયી છે. કારણ કે,View Solution
- 4View Solutionનીચે પૈકી કોણ સંલયન પ્રક્રિયા માટે યોગ્ય છે?
- 5$ {M_p} $ પ્રોટોનનું દળ અને $ {M_n} $ ન્યુટ્રોનનું દળ દર્શાવે છે. આપેલ ન્યુકિલયસની બંધન ઊર્જા $B,$ $Z$ પ્રોટોન અને $N$ ન્યુટ્રોન છે. ન્યુક્લિયસનું દળ $M(N, Z)$ શેના વડે દર્શાવાય? ($c$ એ પ્રકાશનો વેગ છે)View Solution
- 6View Solutionન્યુક્સિયસનું વિખંડન શક્ય છે કારણ કે તેમની ન્યુક્લિઓન દીઠ બંધન ઊર્જા ..........
- 7$ {O^{16}} $ અને $ {O^{17}} $ માટે ન્યુકિલઓન દીઠ બંઘનઊર્જા $7.97\, Mev$ અને $7.75\, Mev$ છે. તો $ {O^{17}} $ માં એક ન્યુટ્રોનને મૂકત કરવા કેટલી ઊર્જાની જરૂર પડશે?View Solution
- 8રેડિયો એકિટવ પદાર્થની એકિટવિટી $30\;min$ માં $700 \;\mathrm{s}^{-1}$ થી $500\; \mathrm{s}^{-1}$ થતી હોય તો તેનો અર્ધઆયુષ્ય સમય કેટલા ...........$min$ હશે?View Solution
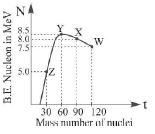
- 9ન્યુક્લિયોન દીઠ બંધન ઊર્જા વિરુદ્ધ પરમાણુદળાંક નો આલેખ આપેલ છે. $W, X, Y$ અને $Z$ ન્યુક્લિયસ ના સ્થાન આપેલા છે. તો કઈ પ્રક્રિયા માં ઊર્જા મુક્ત થાય.View Solution
- 10બે જુદા જુદા એક્ટિવ ન્યુક્લિયસના નમૂનાનો ગુણોત્તર $2:3$ છે. તેનું અર્ધ -આયુષ્ય અનુક્રમે $2$ કલાક અને $3$ કલાક છે. $12$ કલાક બાદ તેમની એક્ટીવીટીનો ગુણોત્તર .......થશે.View Solution
