અહી \(\,{\omega _0} = \,\,0\,,\,\,\alpha \,\, = \,8\,\,rad\,{s^{ - 2}}\)
\( \Rightarrow {\text{ t = 5 s }}\) માટે \(:\, \theta = {\omega _0}t + \frac{1}{2}\alpha {t^2}\,\,\)
\(\Rightarrow \,\,\,{\theta _5} = 0(5) + \frac{1}{2}(8){(5)^2} = 100\,rad\,\,\,\)
\(\therefore \,\,\,{\text{5 s}}\) માં પરિભ્રમનોની સંખ્યા \({n_5} = \frac{{{\theta _5}}}{{2\pi }} = \frac{{100}}{{2\pi }}\)
\({\text{ t = 6 s}}\) માટે \({\theta _6} = (0)(6) + \frac{1}{2}(8){(6)^2} = 144\,\,\,\,\,\therefore \,\,{\text{6s}}\) માં પરિભ્રમનોની સંખ્યા \({n_6} = \frac{{{\theta _6}}}{{2\pi }} = \frac{{144}}{{2\pi }}\)
છઠ્ઠી સેકન્ડમાં પરિભ્રમણોની સંખ્યા = (\(6\ s\) માં થતાં કુલ પરિભ્રમણો) - (\(5\ s\) માં થતાં કુલ પરિભ્રમણો)
છઠ્ઠી સેકન્ડમાં પરિભ્રમણોની સંખ્યા\({\text{ }} = \frac{{144}}{{2\pi }} - \frac{{100}}{{2\pi }} = \frac{{44}}{{2\pi }}\)
છઠ્ઠી સેકન્ડના અંતે કોણીય વેગ \(\omega_6 = \omega_0 +\alpha t = 0 + (8\times 6) = 48\ rad s^{-1}\)
\(6\ s\) જ બાદ ટાર્કનું મૂલ્ય શૂન્ય થાય છે, માટે રિંગ નિયમિત વેગથી ગતિ કરશે. માટે \(\alpha= 0\) થશે.
\(\therefore \theta = {\omega _6}t + \frac{1}{2}\alpha {t^2} = {\omega _6}t = (48)(1)\)
\( = 48\,rad\, = \frac{{48}}{{2\pi }}\) પરિભ્રમન
Download our appand get started for free
Similar Questions
- 1એક વજનદાર તકતી અચળ કોણીય વેગ $\omega$ થી તકતીના સમતલને લંબ અને કેન્દ્રથી પસાર થતી અક્ષને અનુલક્ષીને ફરે છે. તેનું કોણીય વેગમાન $L$ છે. પ્લાસ્ટિકનો એક ટુકડો તકતી પર લંબરૂપે પડે છે અને તેના પર ચોંટી જાય છે તો નીચેનામથી શું અચળ હશે ?View Solution
- 2જો એક તકતીની તેની અક્ષ ને આધારે જડત્વની ચાકમાત્રા $I$ હોય તો તેના તેજ સમતલમાં રહેલા સ્પર્શક ના આધારે તેની જડત્વની ચાકમાત્રા કેટલી થાય $?$View Solution
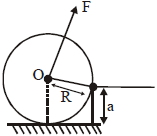
- 3આકૃતિમાં દર્શાવ્યા પ્રમાણે $M$ દળ અને $R$ ત્રિજ્યા ધરાવતો એકસમાન નળાકારને $a$ ($a < R$) ઊંચાઈ પર $F$ જેટલું બળ at its centre $'O'$View Solution
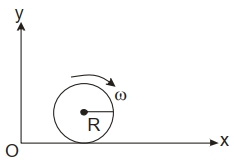
- 4$1 \,kg$ દળ અને $R$ ત્રિજ્યા ધરાવતું એક ગોળાકાર કવચ (Shell) સમક્ષિતિજ સમતલ ઉપર (આકૃતિમાં દર્શાવ્યા અનુસાર) $\omega$ જેટલી કોણીય ઝડપ સાથે ગબડે છે. ઊગમબિંદુ $O$ ને સાપેક્ષ ગોળીય કવચના કોણીય વેગમાનનું મૂલ્ય $\frac{a}{3} R^{2} \omega$ છે. $a$ નું મૂલ્ય ............. હશે.View Solution
- 5બળ $\mathop {\text{F}}\limits^ \to \,\, = \,\,2\hat i\,\, + \;\,\hat j\,\, + \;4\hat k\,$ અને $ \mathop r\limits^ \to \,\, = \,\,7\hat i\,\, + \;3\hat j\,\, + \;\,\hat k\,$ બિંદુ આગળ ટોર્ક ...... હોય.View Solution
- 6એક બોલને $\alpha=6 t^{2}-2 t$ જ્યાં $t$ સેકન્ડમાં અને $\alpha$ એ $rads ^{-2}$ માં છે, થી ફેરવવામાં આવે છે. $t=0$ એ બોલનો કોણીય વેગ $10 \,rads ^{-1}$ અને કોણીય સ્થાન $4 \,rad$ છે. બોલના કોણીય સ્થાન માટેનું સૌથી યોગ્ય સંબંધ_______હશે.View Solution
- 7$2 \,{kg}$ દળ અને $0.6\, {m}$ લંબાઈનો સ્ટીલનો સળિયો ટેબલ પર શિરોલંબ રાખીને નીચેના છેડાને જડિત કરેલ છે અને તે શિરોલંબ સમતલમાં મુક્ત રીતે ભ્રમણ કરી શકે છે. ઉપરના છેડાને ધક્કો આપવામાં આવે છે જેથી સળિયો ગુરુત્વાકર્ષણ અસર હેઠળ નીચે આવે, તેના નીચલા જડિત છેડાના કારણે થતાં ઘર્ષણને અવગણતા, સળિયાનો મુક્ત છેડો જ્યારે તેના સૌથી નીચી સ્થિતિમાંથી પસાર થાય છે ત્યારે તેની ઝડપ (${ms}^{-1}$ માં) કેટલી હશે?. ($g =10\, {ms}^{-2}$ લો )View Solution
- 8ત્રણ સમાન પાતળી લાકડી જેની લંબાઈ $l$ અને દળ $M$ છે તેને જોડીને $H$ અક્ષર બનાવવામાં આવે તો તંત્ર ની $H $ ની કોઈ એક બાજુને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય $?$View Solution
- 9$l$ લંબાઈના એક સળિયાના દ્રવ્યમાન કેન્દ્રથી $\frac{l}{4}$ અંતરે તેને લંબ અક્ષ માથી પસાર થતી અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા કેટલી થાય?View Solution
- 10View Solutionએક કણ નિયમિત વર્તુળાકાર ગતિ માંથી પસાર થાય છે. વર્તુળના સમતલ માં ક્યા બિંદુ એ કણનો કોણીય વેગમાન સંરક્ષિત (અચળ) હશે ?
