$2 \,{kg}$ દળ અને $0.6\, {m}$ લંબાઈનો સ્ટીલનો સળિયો ટેબલ પર શિરોલંબ રાખીને નીચેના છેડાને જડિત કરેલ છે અને તે શિરોલંબ સમતલમાં મુક્ત રીતે ભ્રમણ કરી શકે છે. ઉપરના છેડાને ધક્કો આપવામાં આવે છે જેથી સળિયો ગુરુત્વાકર્ષણ અસર હેઠળ નીચે આવે, તેના નીચલા જડિત છેડાના કારણે થતાં ઘર્ષણને અવગણતા, સળિયાનો મુક્ત છેડો જ્યારે તેના સૌથી નીચી સ્થિતિમાંથી પસાર થાય છે ત્યારે તેની ઝડપ (${ms}^{-1}$ માં) કેટલી હશે?. ($g =10\, {ms}^{-2}$ લો )
JEE MAIN 2021, Diffcult
Download our app for free and get started
a
by energy conservation \({mg} \ell=\frac{1}{2} {I} \omega^{2}=\frac{1}{2} \frac{{m} \ell^{2} \omega^{2}}{3}\)
by energy conservation \({mg} \ell=\frac{1}{2} {I} \omega^{2}=\frac{1}{2} \frac{{m} \ell^{2} \omega^{2}}{3}\)
\(\Rightarrow \omega=\sqrt{\frac{6 {g}}{\ell}}\)
Speed \({v}=\omega {r}=\omega \ell=\sqrt{6 {g} \ell}\)
\({v}=\sqrt{6 \times 10 \times .6}=6\, {m} / {s}\)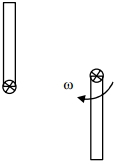
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઢોળાવવાળા સમતલ પર અમુક ઉંચાઈ નળાકાર ચઢે છે અને પછી ગબડીને નીચે આવે છે. (સમગ્ર ગતિ દરમિયાન સરકતો નથી.) નળાકાર પર લાગતા ઘર્ષણ બળની દિશા કઈ છે.
- 2View Solutionસમાન દળ અને ત્રિજયા ધરાવતી તકતી અને રિંગની પોતાની અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજયાનો ગુણોત્તર કેટલો થાય?
- 3$5 \,kg$ અને $2 \,kg$ દળો ધરાવતા બે બ્લોક ને એક અવગણ્ય દળ ધરાવતી સ્પ્રિગ વડે જોડવામાં આવે છે અને તેને એક ધર્ષણ રહિત સમક્ષિતિજ સપાટી પર મૂકવામાં આવે છે. આઘાતએે ભારે બ્લોકને હલકાં બ્લોકની દિશામાં $7 \,m / s$ નો વેગ આપે છે. તો દ્રવ્યમાન કેન્દ્ર નો વેગ ......... $m / s$ થાય?View Solution
- 4જો પૃથ્વીનું દળ અચળ રાખી ત્રિજ્યા અડધી કરવામાં આવે તો દિવસનો સમયગાળો ........ $hr$ થશે.View Solution
- 5View Solutionએક પાતળી, સમક્ષિતિજ વર્તુળાકાર તક્તી, તેના કેન્દ્રમાંથી પસાર થતી ઊર્ધ્વ અક્ષની સાપેક્ષે ગતિ કરે છે. તક્તીની કિનારી પર એક કીટક સ્થિર સ્થિતિમાંથી તકતીના વ્યાસ પર વ્યાસના બીજા અંત્યબિંદુ તરફ ગતિ શરૂ કરે છે. કીટકની આ મુસાફરી દરમિયાન તકતીની કોણીય ઝડપ ……..
- 6ગોળાકાર પ્લેટફોર્મને ઘર્ષણ રહિત શિરોલંબ ધરી પર જડેલ છે. તેની ત્રિજ્યા $R=2\,m$ અને તેની ધરીને અનુલક્ષીને જડત્વની ચાકમાત્રા $200\,kgm^{2}$ છે. તે શરૂઆતમાં સ્થિર છે. $50\,kg$ દળનો વ્યક્તિ આ પ્લેટફોર્મની ધાર પર ઊભો છે અને ધાર પર $1\,ms^{-1}$ના વેગથી જમીનની સાપેક્ષે ચાલવાનું શરૂ કરે છે. આ વ્યક્તિ દ્વારા એક ભ્રમણ પૂર્ણ કરવામાં કેટલો સમય લાગે?View Solution
- 7એક ઢોળાવ યુક્ત્ત સમતલ સમક્ષિતિજ સાથે $30^{\circ}$ નો ખૂણો બનાવે છે. એક નક્કર ગોળો આ ઢોળાવ યુક્ત સમતલ પર સ્થિર સ્થિતિમાંથી સરક્યાં વિના નીચે ગબડ છે ત્યારે તેનો રેખીય પ્રવેગ ........ બરાબર હશે.View Solution
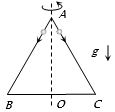
- 8View Solutionસમબાજુની બાજુ પર બે રિંગ સરકે છે. તો નીચેનામાંથી કયા જોડનું સંરક્ષણ થશે?
- 9View Solutionજ્યારે કોઈ પદાર્થ ખરબચડી સમક્ષિતિજ સપાટી ઊપર સરક્યાં વિના (લપસ્યા વિના) ગબડે છે, ત્યારે ઘર્ષણ વડે થતું કાર્ય શું હશે?
- 10$200 g$ અને $500 g$ દળવાળા કણો $10\,\hat i\,\,m/s\,$ અને $3\,\hat i + 5\,\hat j\,\,m/s $ અનુક્રમે ના વેગથી ગતિ કરે છે, તો કણોથી બનતા તંત્રના દ્રવ્યમાન કેન્દ્ર નો વેગ .................. થાય.View Solution