નીચે આપેલા વિકલ્પોમાંથી સાચો ઉતર પસંદ કરો.
(A)
\(B _{ ab }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } \text { (out of the plane) }\)
\(B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(2 \pi) \text { (in the plane) }\)
\(B _{ de }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } \text { (out of the plane) }\)
Hence magnetic field at \(O\) is
\(B _0=-\frac{\mu_0}{4 \pi} \frac{ I }{ r }+\frac{\mu_0}{4 \pi} \frac{ I }{ r }(2 \pi)-\frac{\mu_0}{4 \pi} \frac{ I }{ r }\)
\(B _0=\frac{\mu_0}{2 \pi} \frac{ I }{ r }(\pi-1) \ldots \ldots . . \text { (III) }\)
(B)
\(B _{ ab }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } \text { (out of the plane) }\)
\(B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi) \text { (out of the plane) }\)
\(B _{ de }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } \text { (out of the plane) }\)
Hence magnetic field at \(O\) is
\(B _0=\frac{\mu_0}{4 \pi} \frac{ I }{ r }+\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi)+\frac{\mu_0}{4 \pi} \frac{ I }{ r }\)
\(B _0=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi+2) \ldots .( I )\)
(C)
\(B _{ ab }=\frac{\mu_0}{4 \pi} \frac{ I }{ r } \text { (in the plane) }\)
\(B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi) \text { (in the plane) }\)
\(B _{ de }=0 \text { (at the axis) }\)
Hence magnetic field at \(O\) is
\(B _0=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(1+\pi) \ldots(IV)\)
\(B _{ ab }=0 \text { (at the axis) }\)
\(B _{ bcd }=\frac{\mu_0}{4 \pi} \frac{ I }{ r }(\pi) \text { (out of the plane) }\)
\(B _{ de }=0 \text { (at the axis) }\)
Hence magnetic field at \(O\) is
\(B _0=\frac{\mu_0 I }{4 r } \ldots \text { (II) }\)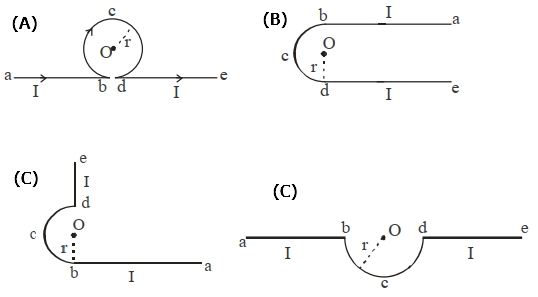
Download our appand get started for free
Similar Questions
- 1View Solutionબે પ્રોટોન કિરણાવલી એકબીજાને સમાંતર એક જ દિશામાં ગતિ કરે છે તો ,...
- 2$1 \,MeV$ ની ઊર્જા ધરાવતો પ્રોટોન નિયમિત ચુંબકીયક્ષેત્રમાં $R$ ત્રિજ્યા ધરાવતા વર્તુળાકાર પથ પર ગતિ કરે છે. $\alpha$ કણની ઉર્જા .......$MeV$ હોવી જોઈએ કે જેથી તે સમાન ત્રિજ્યાના પથમાં સમાન ક્ષેત્રમાં આગળ વધી શકે?View Solution
- 3$2\%$ પ્રવાહ પસાર થતાં ગેલ્વેનોમીટર સાથે $5\, \Omega$ નો શંટ અવરોધ જોડેલો છે. આપેલ ગેલ્વેનોમીટરનો અવરોધ ($\Omega$ માં) કેટલો હશે?View Solution
- 4કોઈ વિસ્તારમાં ચુંબકીય ક્ષેત્ર $\vec{B}=B_0\left(1+\frac{x}{l}\right) \hat{k}$ અસ્તિત્વ ધરાવે છે.$l$ બાજુની અને $i$ વિદ્યુતપ્રવાહ ધરાવતી એક ચોરસ રીંગ તેની બાજુઓ $x-y$ અક્ષને સમાંતર રહે તે રીતે.રીંગ વડે અનુભવતા કુલ ચુંબકીય બળની માત્રા શોધો.View Solution
- 5$ ({\pi ^2}) $ લંબાઇ અને $2\,A$ પ્રવાહધારિત તારથી $1\,cm$ અંતરે ચુંબકીયક્ષેત્ર $B_1$ છે.હવે તારને વર્તુળાકારમાં વાળતાં કેન્દ્ર પર ચુંબકીયક્ષેત્ર $B_2$ છે.તો $ \frac{{{B_2}}}{{{B_1}}} =$View Solution
- 6અર્ધ-આવર્તન રીત થી ગેલ્વેનોમીટરનો અવરોધ માપવાના પ્રયોગમાં, આક્રુતિમાં દર્શાવ્યા અનુસાર, $1 / \theta$ વિધુત અવરોધ પેટીનો અવરોધ ($R$) નો આલેખ મળે છે. ગેલ્વેનોમીટર માટે ગુણવતા અંક (figure of merit) . . . . . .$\times 10^{-1} \mathrm{~A} /$ વિભાગ મળે છે. [ઉદગમનું emf $2V$ છે]View Solution
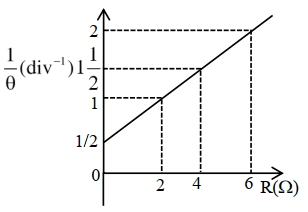
- 7View Solutionએકબીજાને સમાંતર રહેલા વિદ્યુતતંત્ર અને ચુંબકીયક્ષેત્રમાં સ્થિર વિદ્યુતભારિત કણ મુક્તા તેનો ગતિપથ ....
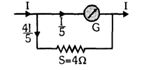
- 8જ્યારે $4\,\Omega$ ના શંટને ગેલ્વેનોમીટર સાથે જોડવામાં આવે તો વિચલન $1/5$ જેટલું ઘટે છે. જો વધારાનો $2\,\Omega$ નો શંટ જોડવામાં આવે તો વિચલન કેટલું હશે ?View Solution
- 9$I$ જેટલો વિદ્યુતપ્રવાહ વહેતા અને $r$ ત્રિજ્યા ધરાવતા એક વર્તુળાકાર ગુંચળાનાં કેન્દ્ર આગળ ચુંબકીય ક્ષેત્ર $B$ છે. તેની અક્ષ ઉપર કેન્દ્ર થી $\frac{ r }{2}$ અંતરે રહેલા બિંદુ આગળ ચુંબકીય ક્ષેત્ર ....... હશેView Solution
- 10એક ગેલ્વેનોમીટરનો અવરોધ $50 \Omega$ છે અને તે મહતમ $5 \mathrm{~mA}$ પ્રવાહને પસાર થવા દે છે.તેનું $100 \mathrm{~V}$ માપી શકે તેવા વોલ્ટ મીટરમાં રુંપાંતર કરવા માટે જોડવો પડતો જરૂરી શ્રેણી અવરોધ______$\Omega$છે.View Solution
