$t = 0$ સમયે જમીન પરના બિંદુ $ P$ માંથી $m$ દળનો કણ $ v_0$ વેગથી $45^°$ ના ખૂણે સમિક્ષિતિજમાં પ્રક્ષેપિત કરવામાં આવે છે. $t\,\, = \,\,\frac{{{v_0}}}{g}$ સમયે કણનું કોણીય વેગમાનનું મૂલ્ય શોધો.
Diffcult
c
પ્રક્ષેપિત પદાર્થ પર ફક્ત તેનું વજન\(mg\) લાગે છે.
પ્રક્ષેપિત પદાર્થ પર ફક્ત તેનું વજન\(mg\) લાગે છે.
તેથી \(t \) સમયે \(mg\) નું \(p\) પાસેટોર્ક \(\tau \,\,\, = \,\,mgd\,\,\, = \,\,mg\,\, \frac{{{v_0}}}{{\sqrt 2 }}\,\, \times \,\,t\)
કોણીય વેગમાનમાં ફેરફાર = કોણીય આઘાત
\(\Delta \,L\,\, = \,\,\int\limits_0^t \tau \,dt\,\,\, = \,\,\,\frac{{mg{v_0}}}{{\sqrt 2 }}\,\,\int\limits_0^t t \,dt\,\,\, = \,\,\frac{{mg{v_0}}}{{\sqrt 2 }}\,\frac{{{t^2}}}{2}\,\, = \,\,\frac{1}{{2\sqrt 2 }}\,.\,\,\frac{{mv_0^3}}{g}\)
\(P\) પાસે પ્રારંભિક કોણીય વેગમાન શૂન્ય છે (રેખીય વેગમાનની કાર્ય રેખા \(P\) માંથી પસાર થાય છે)
તેથી \(t\,\, = \,\,\frac{{{v_0}}}{g}\) સમયે કોણીય વેગમાન \(\frac{1}{{2\sqrt 2 }}\,.\,\,\frac{{mv_0^3}}{g}\) છે અને તેની દિશા પેપરના સમતલને લંબ અંદર જતી દિશામાં છે.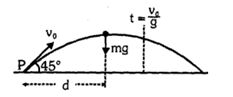
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionગુરૂત્વાકર્ષકની અસર હેઠળ શિરોલંબ રીતે અધોદિશામાં પડતો પદાર્થ બે અસમાન દળોનાં ટુકડાંઓમાં વિભાજિત થાય છે. બંને ટુકડાઓનું એક સાથે લેવામાં આવેલું દ્રવ્યમાન કેન્દ્ર શું થાય?
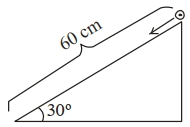
- 2$30^{\circ}$ ખૂણો અને $60\,cm$ લંબાઈવાળા ઢળતા સમતલની ટોચ પરથી એક નક્કર નળાકારને સ્થિર સ્થિતિમાંથી સિલિન્ડર મુક્ત કરવામાં આવે છે. જો નળાકાર સરક્યાં વગર ગબડે છે, તો ઢોળાવવાળા સમતલના તળિયે પહોંચતા તેની ઝડપ $(ms ^{-1}$ માં) કેટલી થાય? (આપેલ $g =10\,ms ^{-2}$)View Solution
- 3View Solutionએક નક્કર ગોળો અવકાશમાં ચાકગતિ કરી રહ્યો છે, જો ગોળાનું દળ અચળ રાખીને તેની ત્રિજ્યા વધારવામાં આવે, તો નીચેનામાંથી કઈ ભૌતિક રાશિ બદલાશે નહિ ?
- 4તકતીની $R_1$ અને $R_2$ આંતરીક અને બાહ્ય ત્રિજ્યા છે. તે અચળ કોણીય ઝડપ થી સરક્યા વિના ગબડે છે. રિંગના અંદર અને બહારના ભાગ પર રહેલા બે કણો દ્વારા અનુભવાતા બળનો ગુણોત્તર $F_1$/$F_2$ શું થશે ?View Solution
- 5$L$ લંબાઈ અને $ M$ દળના પાતળા સળિયાના એક છેડાથી $ L/3$ અંતરે રહેલાં બિંદુમાંથી પસાર થતી અને સળિયાને લંબ અક્ષ પર જડત્વની ચાકમાત્રા કેટલી થશે ?View Solution
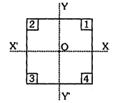
- 6આકૃતિમાં નિયમિત ચોરસ પ્લેટ દર્શાવેલી છે. જેના ખૂણા પરથી ચાર સમાન ચોરસ દૂર કરવામાં આવ્યા છે. ચોરસ $1$ અને $2$ ને દૂર કરતાં $ C.M.$ ક્યાં મળશે ?View Solution
- 7View Solutionવર્તૂળાકાર તકતીને સ્પર્શક તકતીના સમતલમાં રહેલી અક્ષ પર ચક્રાવર્તનની ત્રિજ્યા અને વર્તૂળાકાર રિંગને સ્પર્શક રિંગને સમતલમાં રહેલી અક્ષ પર ચક્રાવર્તનની ત્રિજ્યાનો ગુણોત્તર ......... થશે.
- 8View Solutionજ્યારે દળ, સમતલમાં નિયત બિંદુની ફરતે ચાકગતિ કરતો હોય ત્યારે તેની કોણીય વેગમાનની દિશા ........ હોય.
- 9ગોળાકાર પ્લેટફોર્મને ઘર્ષણ રહિત શિરોલંબ ધરી પર જડેલ છે. તેની ત્રિજ્યા $R=2\,m$ અને તેની ધરીને અનુલક્ષીને જડત્વની ચાકમાત્રા $200\,kgm^{2}$ છે. તે શરૂઆતમાં સ્થિર છે. $50\,kg$ દળનો વ્યક્તિ આ પ્લેટફોર્મની ધાર પર ઊભો છે અને ધાર પર $1\,ms^{-1}$ના વેગથી જમીનની સાપેક્ષે ચાલવાનું શરૂ કરે છે. આ વ્યક્તિ દ્વારા એક ભ્રમણ પૂર્ણ કરવામાં કેટલો સમય લાગે?View Solution
- 10આકૃતિમાં બતાવ્યા પ્રમાણે ઘનગોલક સપાટી પર રેખીય વેગ $v\,ms^{-1}$ થી ગબડે છે. જો તેને ઢાળ પર સરક્યાં વિના ચડાવવું હોય તો તેના માટે ન્યુનત્તમ વેગ કેટલો હોવો જોઈએ?View Solution

