$t=0$ સમયે, પદાર્થ ${A}$ અને ${B}$ બે ન્યુક્લિયર દ્રવ્યનો બનેલો છે. જ્યાં ${N}_{{A}}(0)=2 {N}_{{B}}(0)$, બંને દ્રવ્યના ક્ષય નિયાતાંક $\lambda$ છે. જ્યાં $A$ નું રૂપાંતર ${B}$ માં અને ${B}$ નું રૂપાંતર ${C}$ માં થાય છે. ${N}_{{B}}({t}) / {N}_{{B}}(0)$ નો સમય $t$ સાથે થતો ફેરફારનો ગ્રાફ કયો છે?
${N}_{{A}}(0)=$ ${t}=0$ સમયે $A$ ના પરમાણુ
${N}_{{B}}(0)=$ ${t}=0$ સમયે $B$ ના પરમાણુ
- A
- B
- C
- D
JEE MAIN 2021, Diffcult
Download our app for free and get started
c
\({A} \rightarrow {B}, {B} \rightarrow {C}\)
\({A} \rightarrow {B}, {B} \rightarrow {C}\)
\(\frac{{d} {N}_{{B}}}{{dt}}=\lambda {N}_{{A}}-\lambda {N}_{{B}}\)
\(\frac{{d} {N}_{{B}}}{{dt}}=2 \lambda {N}_{{B}_{0}} {e}^{-\lambda t}-\lambda {N}_{{B}}\)
\({e}^{-\lambda t}\left(\frac{{d} {N}_{{B}}}{{dt}}+\lambda {N}_{{B}}\right)=2 \lambda {N}_{{B}_{0}} {e}^{-\lambda {t}} \times {e}^{\lambda {t}}\)
\(\frac{{d}}{{dt}}\left({N}_{{B}} {e}^{\lambda t}\right)=2 \lambda {N}_{{B}_{0}}\), on integrating
\({N}_{{B}} {e}^{\lambda t}=2 \lambda {tN}_{{B}_{0}}+{N}_{{B}_{0}}\)
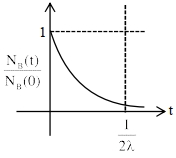
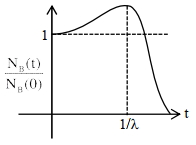
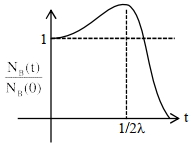
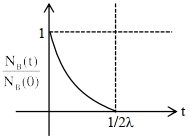
\({N}_{{B}}={N}_{{B}_{0}}[1+2 \lambda {t}] {e}^{-\lambda {t}}\)
\(\frac{{d} {N}_{{B}}}{{dt}}=0\) at \(-\lambda[1+2 \lambda {t}) {e}^{-\lambda {t}}+2 \lambda {e}^{-\lambda {t}}=0\)
\({N}_{{B}_{{max}}}\) at \({t}=\frac{1}{2 \lambda}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1રેડિયો-એક્ટિવ શૃંખલા ક્ષય પ્રક્રિયામાં, પ્રારંભિક ન્યુક્લિયસ ${}_{90}^{232}Th$ છે. અંતે, $6\, \alpha- $કણો અને $4\, \beta -$ કણો ઉત્સર્જન પામે છે. અંત ન્યુકિલયસ ${}_Z^AX\,,\,A$ છે.તો $A $ અને $Z$ કેટલા હશે?View Solution
- 2નીચે ન્યુક્લિયર પ્રક્રિયા આપેલી છે.View Solution
$4\,{\,_1}{H^1}\, \to \,{\,_2}H{e^4} + 2\,{\,_1}{e^0}\, + \,\,2\,v\,\, + 26\,\,MeV\,\,$
- 3$192$ પરમાણુ દળાંક ધરાવતા ન્યુક્લિયસની ત્રિજયા કરતા અડધી ત્રિજયા ધરાવતા ન્યુક્લિયસનો પરમાણુ દળાંક.......View Solution
- 4View Solutionરેડિયો એક્ટિવ તત્વને દર્દીના શરીરમાં દાખલ કરવામાં આવે છે. તે શરીરમાં વિભંજન થઈને વિકિરણ ઉત્પન્ન કરે છે. તેને ડિરેક્ટર દ્રારા વિશ્લેષ્ણ કરવામાં આવે છે. આ સારવારને
- 5બોરોન પર ન્યુટ્રોન આપાત કરતાં $\alpha$ -કણનું ઉત્સર્જન થાય,તો પરિણામી ન્યુકિલયસ કયું બને?View Solution
- 6$t=0$ સમયે રેડિયોએકિટવ તત્ત્વ નમૂનાનું દળ $10\;gm$ છે. બે સરેરાશ જીવનકાળ પછી આ તત્વના નમૂનાનું દળ ($gm$ માં) આશરે કેટલું હશે?View Solution
- 7કોઈ એક ન્યુક્લિયસ માટે બંધન ઊર્જા $18 \times 10^8 \mathrm{~J}$ છે. આપેલ ન્યુક્લિયસ માટે બધા જ ન્યુક્લિઓન્સ અને ન્યુક્લિયસના દળ વચ્ચે કેટલો તફાવત. . . . . . . . . હશે.View Solution
- 8એક રેડિયો એકિટવ દ્વવ્યનો $3$ દિવસમાં તેના મૂળ જથ્થાના $1/8$ માં ભાગ સુધી ધટાડો થાય છે. જો $5$ દિવસ બાદ $8 \times 10^{-3}\,kg$ દ્રવ્ય બાકી રહેતું હોય, તો દ્રવ્યનો પ્રારંભિક જથ્થો ....... $g$ હશે.View Solution
- 9રેડિયોએકિટવ તત્ત્વ દર સેકન્ડે $200$ કણનું ઉત્સર્જન કરે છે, ત્રણ કલાક પછી દર સેકન્ડે $25$ કણનું ઉત્સર્જન કરે છે, તો તેનો અર્ધઆયુ સમય કેટલા .........$ minutes$ હશે?View Solution
- 10View Solutionરેડિયો-ઍક્ટિવ તત્વના ક્ષય દરમિયાન નીચેનામાંથી શું ઉત્સર્જાતું નથી ?