(a)
\(\Delta L=\frac{F L}{A Y}\) \(\left\{\begin{array}{l}\text { Let density of liquid }=\rho \\ \text { Let density of object }=\sigma \\ \text { Mass of object }=M\end{array}\right.\)
\(\Rightarrow\) Elongation \(\propto\) force and force is due to weight
So elongation \(\propto\) weight
\(\Delta L_1 \propto\) weight \(\quad \ldots (1)\) {When not submerged in liquid }
\(\Delta L_2 \propto\) apparant weight \(\ldots .(2)\) {When submerged in liquid }
Dividing \((1)\) by \((2)\)
\(\frac{10}{10-\frac{10}{3}}=\frac{M g}{M g-\frac{M g \rho}{\sigma}}\)
\(\Rightarrow \frac{1}{1-\frac{1}{3}}=\frac{1}{1-\frac{\rho}{\sigma}}\)
Solving this we get
\(\frac{\rho}{\sigma}=\frac{1}{3}\)
So relative densities of object \((\sigma)\) and liquid \((\rho)\) is \(3: 1\)
Download our appand get started for free
Similar Questions
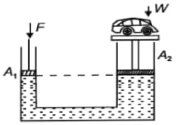
- 1આકૃતિમાં દશાવેલ હાઈડ્રોલિક જેકમાં, કારનું દળ $W=800\,kg , A_1=10 \,cm ^2, A_2=10 \,m ^2$ છે તો કારને ઊંચકવા માટ જરૂરી ન્યૂનતમ બળ $F$ એ .......... $N$ છે?View Solution
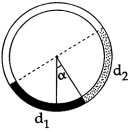
- 2એક વર્તુળાકાર નળી ઊર્ધ્વ સમતલમાં રાખેલ છે.બે પ્રવાહી કે જેઓ એકબીજામાં ભળી શકતા નથી અને તેમની ધનતા $d_1$ અને $d_2$ છે.તેમને આ નળીમાં ભરવામાં આવે છે.દરેક પ્રવાહી કેન્દ્ર આગળ $90°$ નો આંતરિક કોણ રચે છે.જયારે આંતર સપાટીને જોડતી ત્રિજયા શિરોલંબ સાથે $\alpha $ કોણ રચે છે,તો ગુણોત્તર $\frac{{{d_1}}}{{{d_2}}}$View Solution
- 3$d,\,2d$ અને $3d$ ઘનતા ધરાવતા ત્રણ પ્રવાહી સમાન કદ લઇને મિશ્રણ કરવાથી, મિશ્રણની ઘનતા કેટલી થાય?View Solution
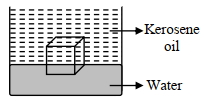
- 4એક બરફનો ચોસલો આંશિંક પાણીમાં અને આંશિક કેરોસીન તેલમાં તરે છે. પાણીમાં ડૂબાડેલ બરફના કદ અને કેરોસીન તેલમાંના બરફના કદનો ગુણોતર. . . . . . .છે (કેરોસીન તેલનુ) વિશિષ્ટ ગુરુત્વ = $0.8$ , બરફનું વિશિષ્ટ ગુરુત્વ =$0.9$) :View Solution
- 5બરફની ઘનતા $0.9 \,g / cm ^3$ છે. તો પાણીની બહાર તરતા બરફનું ......... $\%$ કદ બહાર હશે ?View Solution
- 6$R$ ત્રિજયાના નક્કર ગોળાની અંદર $r$ ત્રિજ્યાનો પોલો ભાગ છે જે લાકડાના વહેરથી ભરેલો છે.નક્કર અને લાકડાના વહેરની સાપેક્ષ ઘનતા $2.4$ અને $0.3$ છે.સંપૂર્ણ કદ પાણીની અંદર હોય તે રીતે ગોળાને તરવા માટે નક્કર અને લાકડાના વહેરના દળનો ગુણોત્તર કેટલો હોવો જોઈએ?View Solution
- 7ઓરડાના તાપમાને તેલની ટાંકીમાં પડતા $5\,mm$ ત્રિજ્યાના તાંબાના બોલનો ટર્મિનલ વેગ $10\,cm-s ^{-1}$ છે. જો ઓરડાના તાપમાને તેલની સ્નિગ્ધતા $0.9\,kg\,m ^{-1}s ^{-1}$ હોય, તો શ્યાનતા બળ કેટલું હશે?View Solution
- 8એક ટાંકીમાં $20 \,^oC$ તાપમાને ભરેલા તેલમાં થઈને પતન પામતા $ 2.0\, mm$ ત્રિજ્યાના એક કૉપર. બૉલનો અંતિમ વેગ $6.5\, cm\, s^{-1}$ છે. $20 \,^oC$ તાપમાને તેલની શ્યાનતા ગણો. તેલની ઘનતા $1.5 \times 10^3\, kg\, m^{-3}$ છે, તાંબાની ઘનતા $8.9\times 10^3\,kg\,m^{-3}$ છે.View Solution
- 9View Solutionતરલ તેની પોતાની જાતે જ વહનનો વિરોધ કરે તેને શું કહે છે ?
- 10સમાન દળના પાણી $1 g / cm^3$ અને $2 g / cm^3$ ઘનતા ધરાવતા પ્રવાહીને મિશ્રણ કરવાથી મિશ્રણની ઘનતા ($ g / cm^3$ માં) કેટલી થાય?View Solution
