તારના બે છેડા વચ્ચે સમાન વૉલ્ટેજ લગાવેલ છે, તેમાં ઉષ્મા ઉત્પન્ન થાય છે,બમણી ઉષ્મા ઉત્પન્ન કરવા માટે ....
AIIMS 2012, Medium
b
\(R=\frac{\rho \ell}{\pi r^{2}}\)
\(R=\frac{\rho \ell}{\pi r^{2}}\)
When \(\ell\) is \(\frac{\ell}{2}\) and radius is \(\frac{\mathrm{r}}{2}\)
\(\therefore \quad \mathrm{R}^{\prime}=\frac{\rho \ell{4}}{\pi 2 \mathrm{r}^{2}}=\frac{2 \rho \ell}{\pi \mathrm{r}^{2}}\)
So, \(\mathrm{R}^{\prime}=2 \mathrm{R}\) So, heat is doubled according to \(\mathrm{H}=\mathrm{I}^{2} \mathrm{RT}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionઆપેલ પરિપથમાં....
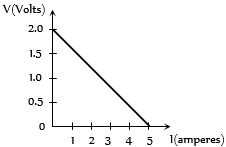
- 2બેટરીનો ટર્મિનલ વોલ્ટેજ અને પ્રવાહનો આલેખ આપેલ છે.તો $emf $ અને આંતરિક અવરોધ કેટલો થાય?View Solution
- 3$1000 \;\Omega$ માં સુવાહકને $10\,V$ વિદ્યુતસ્થિતિમાનનો તફાવત આપવામાં આવે છે. તો $300\,s$ માં સુવાહકમાંથી પસાર થતાં ઈલેક્ટ્રોનની સંખ્યા કેટલી હશે?View Solution
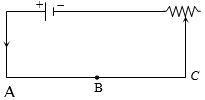
- 4આપેલ પરિપથમાં $AB$ અને $BC$ ની લંબાઇ સમાન છે, $AB$ ની ત્રિજયાના $BC$ કરતાં ત્રણ ગણી છે,તો $AB$ અને $BC$ વિદ્યુતસ્થિતિમાનનો ગુણોત્તર કેટલો થાય?View Solution
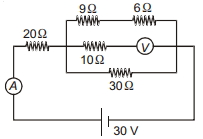
- 5View Solutionનીચે દર્શાવેલ પરિપથમાં વોલ્ટમીટર અને એમિટરનું વાંચન શું હશે?
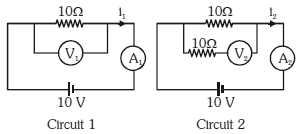
- 6$R$ અવરોધના નિયમિત તારના બનેલા $n$ બાજુવાળા બહુકોણના બે ક્રમિક ખૂણાઓ વચ્ચેનો સમતુલ્ય અવરોધ $............$ થશે.View Solution
- 7$10$ બલ્બને $220\,V$ સપ્લાય સાથે શ્નેણીમાં લગાવ્યા છે.એક બલ્બ ઊડી જવાથી બાકીના બલ્બ શ્નેણીમાં લગાવતા પ્રકાશની તીવ્રતા...View Solution
- 8આપેલ પરિપથમાં $A$ અને $B$ બિંદુ વચ્ચેનો વોલ્ટેજ કેટલો .......... $V$ થાય?View Solution
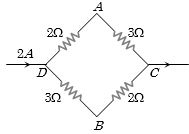
- 9$5\;ampere$ નો ફયૂઝ વાયર મહત્તમ $1\; watt$ જેટલો પાવર સહન કરી શકે છે. ફયૂઝ વાયરનો અવરોધ કેટલો હશે?View Solution
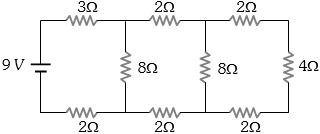
- 10આકૃતિમાં દર્શાવેલ પરિપથમાં જો એમીટર અને વોલ્ટમીટર આદર્શ હોય તો, $9 \Omega$ અવરોધમાં શોષતો પાવર $.......... W$ હશે.View Solution