ત્રિપરિમાણીય યામોમાં ગતિ કરતાં એક કણનાં સ્થાન યામોને
$x = a\,cos\,\omega t$ ,
$y = a\,sin\,\omega t$
અને $z = a\omega t$
વડે આપવામાં આવે છે. તો આ કણની ઝડપ કેટલી થશે?
JEE MAIN 2019, Medium
a
\(\mathrm{v}_{\mathrm{x}}=\frac{\mathrm{d} \mathrm{x}}{\mathrm{dt}}=-\mathrm{a} \omega \sin \omega \mathrm{t}\)
\(\mathrm{v}_{\mathrm{x}}=\frac{\mathrm{d} \mathrm{x}}{\mathrm{dt}}=-\mathrm{a} \omega \sin \omega \mathrm{t}\)
\(\mathrm{v}_{\mathrm{y}}=\frac{\mathrm{dy}}{\mathrm{dt}}=\mathrm{a\omega} \cos \omega \mathrm{t}\)
\(\mathrm{v}_{\mathrm{z}}=\frac{\mathrm{d} z}{\mathrm{dt}}=\mathrm{a} \omega\)
\(\therefore \quad \mathrm{v}=\sqrt{\mathrm{v}_{\mathrm{x}}^{2}+\mathrm{v}_{\mathrm{y}}^{2}+\mathrm{v}_{\mathrm{z}}^{2}}=\mathrm{a} \omega \sqrt{2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$121\,cm$ અને $100\,cm$ લંબાઈ ધરાવતા બે લોલકો સમાન કળામાં દોલનો કરવાનું શરૂ કરે છે. કોઈક ક્ષણે, તેઓ સમાન કળામાં, તેઓના મધ્યસ્થાને છે. આ બંને ફરીવાર સમાન કળામાં તેમનાં સરેેાશ સ્થાન (મધ્ય સ્થાને) હોય તે માટે ટૂંકા લોલક દ્વારા જરૂરી લઘુત્તમ સંખ્યાના દોલનોની સંખ્યા $.....$હશે.View Solution
- 2અવગણ્ય દ્રવ્યમાન ધરાવતી એક પ્લાસ્ટિકની બોટલમાં $310\, ml$ પાણી ભરેલ છે અને તેને શાંત પાણી ભરેલ તલાબમાં તરતી મુકવામાં આવે છે. જો થોડુક નીચે તરફ દબાવીને છોડી દેવામાં આવે તો તે $\omega$ જેટલી કોણીય આવૃત્તિથી સરળ આવર્ત ગતિ શરૂ કરે છે. આ બોટલની ત્રિજ્યા $2.5\, cm$ છે, તો કોણીય આવૃત્તિ $\omega$ ..... $rad\, s^{-1}$ ની નજીકની હશે.View Solution
(પાણીની ઘનતા $=10^3\, kg/m^3$ આપેલ છે.)
- 3બળપ્રેરિત દોલનોમાં કણનો કંપવિસ્તાર બળની $\omega_{1}$ આવૃતિ માટે મહત્તમ, જ્યારે બળની $\omega_{2}$ આવૃતિ માટે ઉર્જા મહત્તમ હોય, તોView Solution
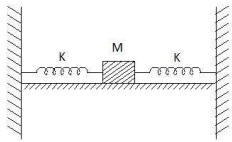
- 4નીચે આપેલ આકૃતિમાં $M = 490\,g$ દળ ધરાવતા બ્લોકને ધર્ષણરહિત ટેબલ ઉપર સમાન સ્પ્રિંગ અચળાંક $\left( K =2\,N\,m ^{-1}\right)$ ધરાવતી બે સ્પ્રિંગો સાથે જોડવામાં આવેલ છે. જો બલોક ને $X\; m$ થી સ્થાનાંતરીત કરવામાં આવે છે તો તેના દ્વારા $14\,\pi$ સેકન્ડમાં થતા પૂર્ણ દોલનોની સંખ્યા $...............$ થશે.View Solution
- 5$1 \,m $ લંબાઈવાળું એક સાદુ લોલક $10 \,rad/s$ કોણીય આવૃત્તિથી દોલન કરે છે. લોલકનો આધાર $1 \,rad/s$ જેટલી નાની કોણીય આવૃત્તિ અને $10^{-2}\, m$ જેટલા કંપવિસ્તારથી ઉપર નીચે દોલન કરવાનું શરૂ કરે છે. લોલકની કોણીય આવૃત્તિમાં થતા સાપેક્ષ ફેરફારને _______ દ્વારા સચોટ રીતે દર્શાવી શકાયView Solution
- 6સાદુ લોલક $2 \,sec$ ના આવર્તકાળથી દોલનો કરે છે,સમતોલન સ્થાન પાસે દોરીમાં તણાવ કેટલો થાય?View Solution
- 7એક સ.આ. દોલકનો મહત્તમ વેગ અને મહત્તમ પ્રવેગ અનુક્રમે $\beta $ અને $\alpha $ છે, તો તેની આવૃત્તિ કેટલી હશે ?View Solution
- 8$y(cm) = \sin \frac{\pi }{2}\left( {\frac{t}{2} + \frac{1}{3}} \right).$ સરળ આવર્તગતિ કરતા પદાર્થનો મહતમ પ્રવેગ કેટલો ..... $cm/sec^2$ થાય?View Solution
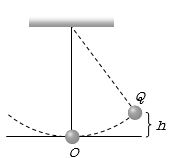
- 9એક લોલકના દોલકને સમક્ષિતિજ સ્થિતિ આગળથી મુક્ત કરવામાં આવે છે, લોલકની લંબાઈ $10 \mathrm{~m}$ છે. જો દોલકની $10 \%$ ઊર્જા એ હવાના અવરોધની સામે વેડફાતી હોય તો તે જ્યારે નીચેના ન્યૂનતમ બિંદુ આગળ પહાંચે ત્યારે દોલક ની ઝડ૫_______થશે.${ [g: } 10 \mathrm{~ms}^{-2}${ નો ઉપયોગ કરો] }View Solution
- 10$L$ લંબાઇનો તાર છત પર બાંધેલ છે. બીજા છેડા પર $k$ બળઅચળાંક ઘરાવતી સ્પ્રિંગ સાથે બાંધેલ છે. $m$ દળનો પદાર્થ સ્પ્રિંગ સાથે બાંધેલ છે.તારનો આડછેદ $A$ અને યંગમોડયુલસ $Y$ છે. $m$ દળને ખેંચીને મૂકત કરતા સરળ આવર્તગતિનો આવર્તકાળ કેટલો થાય?View Solution
