ત્રણ સમકેન્દ્રિયો ધાતુ કવચો $A,B$ અને $C$ ની અનુક્રમે ત્રિજયાઓ $a,b$ અને $c$ $( a < b < c)$ ની પૃષ્ઠ વિદ્યુતભાર ઘનતાઓ અનુક્રમે $ + \sigma , - \sigma $ અને $ + \sigma $ છે. $B$ કવચનું સ્થિતિમાન :
JEE MAIN 2018, Diffcult
a
Potential outside the shell, \(V_{outside}\) \(=\frac{\mathrm{KQ}}{\mathrm{r}}\)
Potential outside the shell, \(V_{outside}\) \(=\frac{\mathrm{KQ}}{\mathrm{r}}\)
where \(\mathrm{r}\) is distance of point from the centre of shel Potential inside the shell, \(V_{\text {inside }}=\frac{K Q}{R}\)
where \('R"\) is radius of the shell
\(\mathrm{V}_{\mathrm{B}}=\frac{\mathrm{Kq}_{\mathrm{A}}}{\mathrm{r}_{\mathrm{b}}}+\frac{\mathrm{Kq}_{\mathrm{B}}}{\mathrm{r}_{\mathrm{b}}}+\frac{\mathrm{Kq}_{\mathrm{C}}}{\mathrm{r}_{\mathrm{c}}}\)
\(\mathrm{V}_{\mathrm{B}}=\frac{1}{4 \pi \epsilon_{0}}\left[\frac{\sigma 4 \pi \mathrm{a}^{2}}{\mathrm{b}}-\frac{\sigma 4 \pi \mathrm{b}^{2}}{\mathrm{b}}+\frac{\sigma 4 \pi \mathrm{c}^{2}}{\mathrm{c}}\right]\)
\(V_{B}=\frac{\sigma}{\epsilon_{0}}\left[\frac{a^{2}-b^{2}}{b}+c\right]\)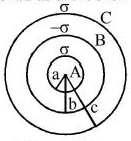
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
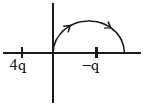
- 1$x-$અક્ષ પર $4 q$ અને $-q$ વિજભાર ધરાવતા બે બિંદુવત વિજભાર $x=-\frac{d}{2}$ અને $x=\frac{d}{2}$ સ્થાને જડેલ છે. જો ત્રીજા $'q'$ જેટલા બિંદુવત વિજભારને આકૃતિમાં દર્શાવ્યા પ્રમાણે ઉગમબિંદુથી $x = d$ સુધી અર્ધવર્તુળાકાર માર્ગ પર લઈ જવામાં આવે છે. તો તે દરમિયાન વિજભારની ઉર્જા....View Solution
- 2એક સંધારક $R$ અવરોધની મદદથી વિદ્યુતભાર રહિત (ડીસ્ચાર્જ) થાય છે. ધારો કે $t_{1}$ સમયમાં સંધારકમાં સંગ્રહીત ઊર્જા ધટીને તેની પ્રારંભિક મૂલ્ય કરતાં અડધી થાય છે અને $t _{2}$ સમયમાં સંગ્રહીત વિદ્યુતભાર ધટીને તેનાં પ્રારંભિક મૂલ્ય કરતા આઠમા ભાગનો થાય છે. $t_{1} / t_{2}$ ગુણોત્તર .............થશે.View Solution
- 3હવામાં એકબીજાથી $1\, m$ અંતરે રહેલા બે બિંદુવત ઋણ વિદ્યુતભારોના તંત્રની સ્થિતિઊર્જા ...... (દરેક વિદ્યુતભારનું મૂલ્ય $2\mu C$ છે)View Solution
- 4કેપેસિટરની બે પ્લેટ વચ્ચે હવા હોેય ત્યારે તેનું કેપેસિટન્સ $1\,pF$ છે.બે પ્લેટ વચ્ચેનું અંતર બમણું કરી તેમની વચ્ચે મીણથી ભરી દેતા નવો કેપેસિટન્સ $2\,pF.$ છે. તો મીણનો ડાયઇલેકટ્રીક અચળાંક કેટલો હશે?View Solution
- 5$A$ અને $B$ બે વાહક ગોળાઓની ત્રિજ્યાઓ અનુક્રમે $1\, mm$ અને $2 \,mm$ છે અને તેઓ વિદ્યુતભારિત કરેલાં છે તથા $5\, cm$ અંતરે રાખેલા છે. હવે તેમને વાહક તારથી જોડતાં સમતોલન સ્થિતિમાં તેમની સપાટી પરનાં વિદ્યુતક્ષેત્રની તીવ્રતાઓનો ગુણોત્તર ...... છે.View Solution
- 6$C_1$ કેપેસિટન્સવાળા કેપેસિટરને $V$ વોલ્ટ સુઘી ચાર્જ કરેલ છે.આ કેપેસિટરને બીજા વિદ્યુતભાર રહિત $C_2$ ક્ષમતાવાળા કેપેસિટર સાથે સમાંતર જોડવામાં આવે છે. દરેક કેપેસિટર પરના વિદ્યુતસ્થિતિમાનનો તફાવત કેટલો થાય?View Solution
- 7વિદ્યુતસ્થિતિમાન $V = 4{x^2}\,volt$ છે.તો $(1m,\,0,\,2m)$ બિંદુ પર વિદ્યુતક્ષેત્ર કેટલું લાગે?View Solution
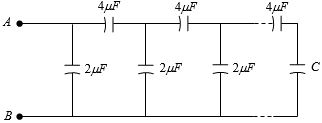
- 8આપેલી આકૃતિમાં $C$ ના ........$\mu F$ મૂલ્ય માટે $A$ અને $B$ વચ્ચેનો સમતુલ્ય કેપેસિટન્સ એ પુનરાવર્તન થતાં વિભાગોની સંખ્યા પર આધાર ન રાખે?View Solution
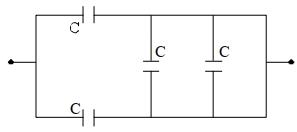
- 9View Solutionદર્શાવેલ સંયોજનની સમતુલ્ય સંધારકતા (કેપેસીટન્સ) ....... છે.
- 10$C$ કેપેસિટન્સવાળા એક સમાંતર પ્લેટ કેપેસિટરને બેટરી સાથે જોડી $V$ સ્થિતિમાને વિદ્યુતભારિત કરવામાં આવે છે. બીજા $2C$ કેપેસિટન્સ ધરાવતા કેપેસિટરને બીજી બેટરી સાથે જોડી $2V$ સ્થિતિમાને વિદ્યુતભારીત કરવામાં આવે છે. આ બેટરીઓને દૂર કર્યા બાદ અને કેપેસિટરોને સમાંતરમાં એવી રીતે જોડવામાં આવે છે કે જેથી એકની ધન પ્લેટ બીજાની ઋણ પ્લેટ સાથે જોડેલી હોય, તો તંત્રની અંતિમ ઉર્જા ગણો.View Solution
